Solved

The Text Describes Logistic Growth with an Equation for the Actual

Question 20

Essay

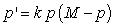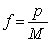The text describes logistic growth with an equation for the actual population in terms of a growth constant and a maximum population (carrying capacity), The text describes logistic growth with an equation for the actual population in terms of a growth constant and a maximum population (carrying capacity), . The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population, . Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum, if k = 0.00100 day<sup>-1</sup> and M = 4000? . The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population, The text describes logistic growth with an equation for the actual population in terms of a growth constant and a maximum population (carrying capacity), . The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population, . Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum, if k = 0.00100 day<sup>-1</sup> and M = 4000? . Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum,
if k = 0.00100 day-1 and M = 4000?

Correct Answer:

verifed

Verified

blured image time(60-80%) = 0.24...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q15: Find the solution of the differential equation,

Q16: Solve the following initial value problem explicitly.

Q17: Use the direction field below to sketch

Q18: Match the appropriate slope field with the

Q19: The rate at which water flows out

Q21: Find all equilibrium points for the following

Q22: The differential equation is separable. Find the

Q23: Write the following third-order equation as a

Q24: Calculate how much you would need to

Q25: Identify the equilibrium solutions for <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg"