Solved

Identify the Equilibrium Solutions for , and Determine If

Question 25

Multiple Choice

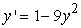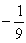Identify the equilibrium solutions for Identify the equilibrium solutions for , and determine if they are stable or unstable. A) y = (unstable) ; y = (stable) B) y = (stable) ; y = (stable) C) y = (stable) ; y = (stable) D) y = (unstable) ; y = (stable) , and determine if they are stable or unstable.


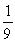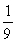A) y = Identify the equilibrium solutions for , and determine if they are stable or unstable. A) y = (unstable) ; y = (stable) B) y = (stable) ; y = (stable) C) y = (stable) ; y = (stable) D) y = (unstable) ; y = (stable) (unstable) ; y = Identify the equilibrium solutions for , and determine if they are stable or unstable. A) y = (unstable) ; y = (stable) B) y = (stable) ; y = (stable) C) y = (stable) ; y = (stable) D) y = (unstable) ; y = (stable) (stable)
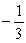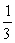B) y = Identify the equilibrium solutions for , and determine if they are stable or unstable. A) y = (unstable) ; y = (stable) B) y = (stable) ; y = (stable) C) y = (stable) ; y = (stable) D) y = (unstable) ; y = (stable) (stable) ; y = Identify the equilibrium solutions for , and determine if they are stable or unstable. A) y = (unstable) ; y = (stable) B) y = (stable) ; y = (stable) C) y = (stable) ; y = (stable) D) y = (unstable) ; y = (stable) (stable)
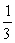C) y = Identify the equilibrium solutions for , and determine if they are stable or unstable. A) y = (unstable) ; y = (stable) B) y = (stable) ; y = (stable) C) y = (stable) ; y = (stable) D) y = (unstable) ; y = (stable) (stable) ; y = Identify the equilibrium solutions for , and determine if they are stable or unstable. A) y = (unstable) ; y = (stable) B) y = (stable) ; y = (stable) C) y = (stable) ; y = (stable) D) y = (unstable) ; y = (stable) (stable)
D) y = Identify the equilibrium solutions for , and determine if they are stable or unstable. A) y = (unstable) ; y = (stable) B) y = (stable) ; y = (stable) C) y = (stable) ; y = (stable) D) y = (unstable) ; y = (stable) (unstable) ; y = Identify the equilibrium solutions for , and determine if they are stable or unstable. A) y = (unstable) ; y = (stable) B) y = (stable) ; y = (stable) C) y = (stable) ; y = (stable) D) y = (unstable) ; y = (stable) (stable)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q20: The text describes logistic growth with an

Q21: Find all equilibrium points for the following

Q22: The differential equation is separable. Find the

Q23: Write the following third-order equation as a

Q24: Calculate how much you would need to

Q26: Use your calculator to construct the direction

Q27: Match the appropriate slope field with the

Q28: Find all equilibrium points for the following

Q29: Solve the following initial value problem explicitly.

Q30: Use Euler's method with h = 0.1