Solved

Use the Given Velocity Function and Initial Position to Estimate

Question 22

Multiple Choice

Use the given velocity function and initial position to estimate the final position Use the given velocity function and initial position to estimate the final position . Round to two decimal places. A) B) C) D) . Round to two decimal places. Use the given velocity function and initial position to estimate the final position . Round to two decimal places. A) B) C) D)


A) Use the given velocity function and initial position to estimate the final position . Round to two decimal places. A) B) C) D)
B) Use the given velocity function and initial position to estimate the final position . Round to two decimal places. A) B) C) D)
C) Use the given velocity function and initial position to estimate the final position . Round to two decimal places. A) B) C) D)
D) Use the given velocity function and initial position to estimate the final position . Round to two decimal places. A) 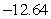B) 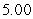C) D)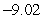

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q17: Use the properties of logarithms to rewrite

Q18: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Evaluate the

Q19: Make the indicated substitution for an unspecified

Q20: Evaluate the derivative using properties of logarithms

Q21: Find the position function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Find

Q23: Approximate the area under the curve on

Q24: Approximate the area under the curve on

Q25: Compute the Trapezoidal Rule approximation by hand

Q26: Find the general antiderivative. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Find

Q27: Translate the following calculation into summation notation