Solved

Find the Position Function from the Given Acceleration Function

Question 21

Multiple Choice

Find the position function Find the position function from the given acceleration function and initial values. Assume that units are feet and seconds. A) B) C) D) from the given acceleration function and initial values. Assume that units are feet and seconds. Find the position function from the given acceleration function and initial values. Assume that units are feet and seconds. A) B) C) D)


A) Find the position function from the given acceleration function and initial values. Assume that units are feet and seconds. A) B) C) D)
B) Find the position function from the given acceleration function and initial values. Assume that units are feet and seconds. A) B) C) D)
C) Find the position function from the given acceleration function and initial values. Assume that units are feet and seconds. A) B) C) D)
D) Find the position function 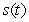from the given acceleration function and initial values. Assume that units are feet and seconds.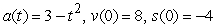 A) 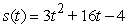B) 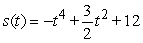C) 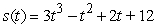D)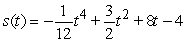

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q16: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Evaluate the

Q17: Use the properties of logarithms to rewrite

Q18: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Evaluate the

Q19: Make the indicated substitution for an unspecified

Q20: Evaluate the derivative using properties of logarithms

Q22: Use the given velocity function and initial

Q23: Approximate the area under the curve on

Q24: Approximate the area under the curve on

Q25: Compute the Trapezoidal Rule approximation by hand

Q26: Find the general antiderivative. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Find