An Alarm Call Benefits Multiple Individuals, Both Related and Unrelated $\sum _ { 1 } ^ { A } r _ { 1 } b _ { i } - c > 0$

Multiple Choice

An alarm call benefits multiple individuals, both related and unrelated (r ? 0) . Can this behavior still evolve according to Hamilton's rule? (There are 1, 2, . . . , A individuals that are related to the donor by r₁, r₂,…, r_A and receive benefits b₁, b₂,…, b_A)

A) No; unrelated individuals will automatically set the benefits to 0, as Hamilton's rule for
Multiple individuals is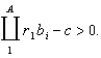

B) No; this case no longer addresses inclusive fitness, and Hamilton's rule does not apply.
C) Yes, if there are more related individuals benefiting than unrelated individuals, as Hamilton's rule for multiple individuals is
$\sum _ { 1 } ^ { A } r _ { 1 } b _ { i } - c > 0$
D) Yes, as long as the benefits to related individuals satisfy
$\sum _ { 1 } ^ { A } r _ { i } b _ { i } - c > 0$