Solved

The Following Data Show the Demand for an Airline Ticket

Question 25

Multiple Choice

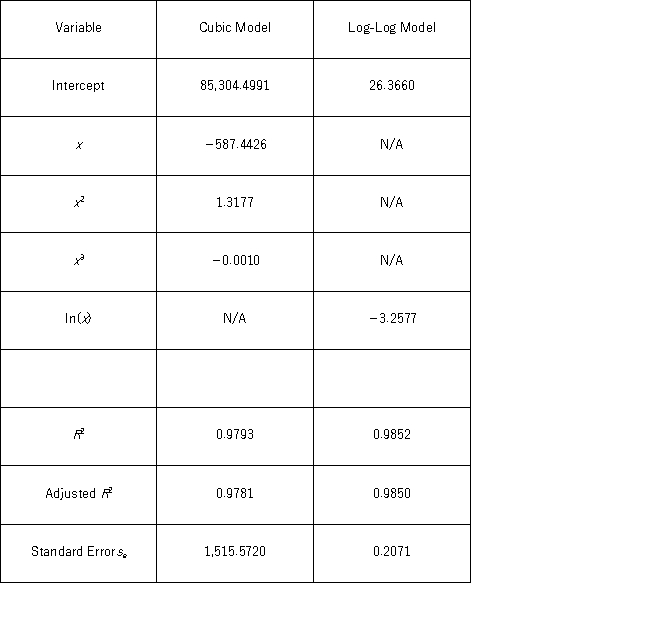The following data show the demand for an airline ticket dependent on the price of this ticket. The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2 </sup>+ β<sub>3</sub>Price<sup>3 </sup>+ ε and ln(Demand) = β<sub>0</sub> + β<sub>1</sub>ln(Price) + ε,the following regression results are available. Assuming that the sample correlation coefficient between Demand and = exp(26.3660 - 3.2577 ln(Price) + (0.2071) <sup>2</sup>/2) is 0.956,what is the percentage of variations in Demand explained by the log-log regression equation? A) 98.52% B) 98.50% C) 91.39% D) 97.93% For the assumed cubic and log-log regression models,Demand = β0 + β1Price + β2Price2 + β3Price3 + ε and ln(Demand) = β0 + β1ln(Price) + ε,the following regression results are available. 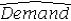The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2 </sup>+ β<sub>3</sub>Price<sup>3 </sup>+ ε and ln(Demand) = β<sub>0</sub> + β<sub>1</sub>ln(Price) + ε,the following regression results are available. Assuming that the sample correlation coefficient between Demand and = exp(26.3660 - 3.2577 ln(Price) + (0.2071) <sup>2</sup>/2) is 0.956,what is the percentage of variations in Demand explained by the log-log regression equation? A) 98.52% B) 98.50% C) 91.39% D) 97.93% Assuming that the sample correlation coefficient between Demand and The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2 </sup>+ β<sub>3</sub>Price<sup>3 </sup>+ ε and ln(Demand) = β<sub>0</sub> + β<sub>1</sub>ln(Price) + ε,the following regression results are available. Assuming that the sample correlation coefficient between Demand and = exp(26.3660 - 3.2577 ln(Price) + (0.2071) <sup>2</sup>/2) is 0.956,what is the percentage of variations in Demand explained by the log-log regression equation? A) 98.52% B) 98.50% C) 91.39% D) 97.93% = exp(26.3660 - 3.2577 ln(Price) + (0.2071) 2/2) is 0.956,what is the percentage of variations in Demand explained by the log-log regression equation?


A) 98.52%
B) 98.50%
C) 91.39%
D) 97.93%

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q20: The equation y = β<sub>0</sub> + β<sub>1</sub>x

Q21: The following Excel scatterplot with the fitted

Q22: Which of the following regression models is

Q24: The log-log and the _ models can

Q27: The cubic regression model allows for two

Q28: A quadratic regression model is a special

Q29: The quadratic and logarithmic models,y = β<sub>0</sub>

Q30: For the log-log model ln(y)= β<sub>0</sub> +

Q56: An inverted U-shaped curve is also known

Q63: The logarithmic model is especially attractive when