Solved

If the Variance of U Is Quadratic in X,then It

Question 44

Multiple Choice

If the variance of u is quadratic in X,then it can be expressed as


A) var(ui|Xi) = If the variance of u is quadratic in X,then it can be expressed as A) var(ui|Xi) = B) var(ui|Xi) = θ0 + θ1 C) var(ui|Xi) = θ0 + θ1 D) var(ui|Xi) =
B) var(ui|Xi) = θ0 + θ1 If the variance of u is quadratic in X,then it can be expressed as A) var(ui|Xi) = B) var(ui|Xi) = θ0 + θ1 C) var(ui|Xi) = θ0 + θ1 D) var(ui|Xi) =
C) var(ui|Xi) = θ0 + θ1 If the variance of u is quadratic in X,then it can be expressed as A) var(ui|Xi) = B) var(ui|Xi) = θ0 + θ1 C) var(ui|Xi) = θ0 + θ1 D) var(ui|Xi) =
D) var(ui|Xi) = If the variance of u is quadratic in X,then it can be expressed as A) var(ui|Xi) = 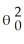B) var(ui|Xi) = θ0 + θ1 C) var(ui|Xi) = θ0 + θ1 D) var(ui|Xi) =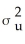

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q6: The advantage of using heteroskedasticity-robust standard errors

Q11: In practice, you may want to use

Q20: "I am an applied econometrician and therefore

Q39: Consider the simple regression model Yi =

Q40: The following is not one of the

Q41: (Requires Appendix material)Your textbook considers various distributions

Q42: The OLS estimator is a linear estimator,

Q42: Besides the Central Limit Theorem, the other

Q43: Assume that the variance depends on a

Q48: If the functional form of the conditional