Solved

Consider the Model Yi = β1Xi + Ui,where Ui =

Question 21

Essay

Consider the model Yi = β1Xi + ui,where ui = c Consider the model Yi = β1Xi + ui,where ui = c 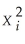ei and all of the X's and e's are i.i.d.and distributed N(0,1). (a)Which of the Extended Least Squares Assumptions are satisfied here? Prove your assertions. (b)Would an OLS estimator of β1 be efficient here? (c)How would you estimate β1 by WLS? ei and all of the X's and e's are i.i.d.and distributed N(0,1).
(a)Which of the Extended Least Squares Assumptions are satisfied here? Prove your assertions.
(b)Would an OLS estimator of β1 be efficient here?
(c)How would you estimate β1 by WLS?

Correct Answer:

verifed

Verified

(a)The extended least squares assumption...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q4: "One should never bother with WLS. Using

Q8: If, in addition to the least squares

Q18: (Requires Appendix material)This question requires you to

Q19: The Gauss-Markov Theorem proves that<br>A)the OLS estimator

Q20: Consider estimating a consumption function from a

Q24: (Requires Appendix material)If the Gauss-Markov conditions hold,then

Q27: What does the Gauss-Markov theorem prove? Without

Q32: All of the following are good reasons

Q37: (Requires Appendix material)State and prove the Cauchy-Schwarz

Q43: Slutsky's theorem combines the Law of Large