Essay
(Requires Appendix material)If the Gauss-Markov conditions hold,then OLS is BLUE.In addition,assume here that X is nonrandom.Your textbook proves the Gauss-Markov theorem by using the simple regression model Yi = β0 + β1Xi + ui and assuming a linear estimator 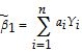 .Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator:
.Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator: 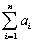 = 0 and
= 0 and 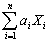 = 1.
= 1.
The variance of the estimator is var( 
 X1,…,Xn)=
X1,…,Xn)= 
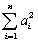 .
.
Different from your textbook,use the Lagrangian method to minimize the variance subject to the two constraints.Show that the resulting weights correspond to the OLS weights.
Correct Answer:

Verified
Define the Lagrangian as follows:
L = 
 ...
...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
L =
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q4: "One should never bother with WLS. Using
Q8: If, in addition to the least squares
Q19: The Gauss-Markov Theorem proves that<br>A)the OLS estimator
Q20: Consider estimating a consumption function from a
Q21: Consider the model Yi = β1Xi +
Q26: One of the earlier textbooks in econometrics,
Q27: What does the Gauss-Markov theorem prove? Without
Q28: In order to use the t-statistic for
Q29: Suppose that the conditional variance is var(ui|Xi)=
Q37: (Requires Appendix material)State and prove the Cauchy-Schwarz