Essay
Consider the model Yi - β1Xi + ui,where the Xi and ui the are mutually independent i.i.d.random variables with finite fourth moment and E(ui)= 0.
(a)Let  1 denote the OLS estimator of β1.Show that
1 denote the OLS estimator of β1.Show that 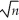 (
( 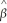 1- β1)=
1- β1)= 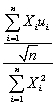 .
.
(b)What is the mean and the variance of 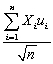 ? Assuming that the Central Limit Theorem holds,what is its limiting distribution?
? Assuming that the Central Limit Theorem holds,what is its limiting distribution?
(c)Deduce the limiting distribution of 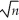 (
( 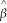 1 - β1)? State what theorems are necessary for your deduction.
1 - β1)? State what theorems are necessary for your deduction.
Correct Answer:

Verified
(a)The OLS estimator in this case is  1 ...
1 ...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q8: If, in addition to the least squares
Q15: (Requires Appendix material)If X and Y are
Q26: One of the earlier textbooks in econometrics,
Q28: In order to use the t-statistic for
Q29: Suppose that the conditional variance is var(ui|Xi)=
Q32: The class of linear conditionally unbiased estimators
Q33: You need to adjust <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2833/.jpg" alt="You
Q34: The following is not part of the
Q35: Homoskedasticity means that<br>A)var(ui|Xi)= <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2833/.jpg" alt="Homoskedasticity means
Q36: Your textbook states that an implication of