Your Textbook States That an Implication of the Gauss-Markov Theorem

Essay

Your textbook states that an implication of the Gauss-Markov theorem is that the sample average, 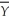,is the most efficient linear estimator of E(Yi)when Y1,... ,Yn are i.i.d.with E(Yi)= μY and var(Yi)= 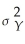.This follows from the regression model with no slope and the fact that the OLS estimator is BLUE.
Provide a proof by assuming a linear estimator in the Y's, 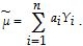(a)State the condition under which this estimator is unbiased.
(b)Derive the variance of this estimator.
(c)Minimize this variance subject to the constraint (condition)derived in (a)and show that the sample mean is BLUE.