The Logit Regression (11

Essay

The logit regression (11.10)on page 393 of your textbook reads: 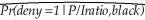= F(-4.13 + 5.37 P/Iratio + 1.27 black)
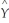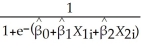(a)Using a spreadsheet program such as Excel,plot the following logistic regression function with a single X, i = where 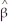0 = -4.13, 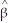1 = 5.37, 2 = 1.27.Enter values for X1 in the first column starting from 0 and then increment these by 0.1 until you reach 2.0.Let X2 be 0 at first.Then enter the logistic function formula in the next column.Next allow X2 to be 1 and calculate the new values for the logistic function in the third column.Finally produce the predicted probabilities for both blacks and whites,connecting the predicted values with a line.
(b)Using the same spreadsheet calculations,list how the probability increases for blacks and for whites as the P/I ratio increases from 0.5 to 0.6.
(c)What is the difference in the rejection probability between blacks and whites for a P/I ratio of 0.5 and for 0.9? Why is the difference smaller for the higher value here?
(d)Table 11.2 on page 401 of your textbook lists logit regressions (column 2)with further explanatory variables.Given that you can only produce simple plots in two dimensions,how would you proceed in (a)above if there were more than a single explanatory variable?