Solved

(Requires Appendix Material and Calculus)The Logarithm of the Likelihood Function

Question 20

Essay

(Requires Appendix material and Calculus)The logarithm of the likelihood function (L)for estimating the population mean and variance for an i.i.d.normal sample is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum):
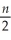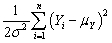L = - (Requires Appendix material and Calculus)The logarithm of the likelihood function (L)for estimating the population mean and variance for an i.i.d.normal sample is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum): L = - log(2πσ2)- Derive the maximum likelihood estimator for the mean and the variance.How do they differ,if at all,from the OLS estimator? Given that the OLS estimators are unbiased,what can you say about the maximum likelihood estimators here? Is the estimator for the variance consistent? log(2πσ2)- (Requires Appendix material and Calculus)The logarithm of the likelihood function (L)for estimating the population mean and variance for an i.i.d.normal sample is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum): L = - log(2πσ2)- Derive the maximum likelihood estimator for the mean and the variance.How do they differ,if at all,from the OLS estimator? Given that the OLS estimators are unbiased,what can you say about the maximum likelihood estimators here? Is the estimator for the variance consistent? Derive the maximum likelihood estimator for the mean and the variance.How do they differ,if at all,from the OLS estimator? Given that the OLS estimators are unbiased,what can you say about the maximum likelihood estimators here? Is the estimator for the variance consistent?

Correct Answer:

verifed

Verified

Taking the derivative with respect to th...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q12: The logit model derives its name from<br>A)the

Q14: The maximum likelihood estimation method produces, in

Q16: The estimated logit regression in your textbook

Q17: When estimating probit and logit models,<br>A)the t-statistic

Q18: The logit regression (11.10)on page 393 of

Q21: Your textbook plots the estimated regression function

Q23: (Requires Advanced material)Nonlinear least squares estimators in

Q24: Consider the following probit regression<br>Pr(Y = 1

Q46: Besides maximum likelihood estimation of the logit

Q50: Earnings equations establish a relationship between an