Essay
You have a limited dependent variable (Y)and a single explanatory variable (X).You estimate the relationship using the linear probability model,a probit regression,and a logit regression.The results are as follows: 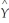 = 2.858 - 0.037 × X
= 2.858 - 0.037 × X
(0.007)
Pr(Y = 1  X)= F (15.297 - 0.236 × X)
X)= F (15.297 - 0.236 × X)
Pr(Y = 1  X)= Φ (8.900 - 0.137 × X)
X)= Φ (8.900 - 0.137 × X)
(0.058)
(a)Although you cannot compare the coefficients directly,you are told that "it can be shown" that certain relationships between the coefficients of these models hold approximately.These are for the slope: 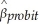 ≈ 0.625 ×
≈ 0.625 ×  ,
,  ≈ 0.25 ×
≈ 0.25 × 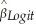 .Take the logit result above as a base and calculate the slope coefficients for the linear probability model and the probit regression.Are these values close?
.Take the logit result above as a base and calculate the slope coefficients for the linear probability model and the probit regression.Are these values close?
(b)For the intercept,the same conversion holds for the logit-to-probit transformation.However,for the linear probability model,there is a different conversion: 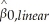 ≈ 0.25 ×
≈ 0.25 × 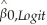 + 0.5
+ 0.5
Using the logit regression as the base,calculate a few changes in X (temperature in degrees of Fahrenheit)to see how good the approximations are.
Correct Answer:

Verified
(a)  ≈ 0.625 × 0.236 = 0.148,which is qu...
≈ 0.625 × 0.236 = 0.148,which is qu...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q1: The linear probability model is<br>A)the application of
Q13: Nonlinear least squares<br>A)solves the minimization of the
Q19: In the linear probability model, the interpretation
Q24: Equation (11.3)in your textbook presents the regression
Q37: In the expression Pr(deny = 1 <img
Q38: F-statistics computed using maximum likelihood estimators<br>A)cannot be
Q39: In the probit regression,the coefficient β1 indicates<br>A)the
Q40: (Requires Appendix material and Calculus)The log of
Q43: (Requires Appendix material)Briefly describe the difference between
Q43: The major flaw of the linear probability