Solved

(Requires Appendix Material and Calculus)The Log of the Likelihood Function

Question 40

Essay

(Requires Appendix material and Calculus)The log of the likelihood function (L)for the simple regression model with i.i.d.normal errors is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum):
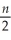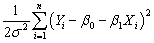L = - (Requires Appendix material and Calculus)The log of the likelihood function (L)for the simple regression model with i.i.d.normal errors is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum): L = - log(2π)- log σ2 - Derive the maximum likelihood estimator for the slope and intercept.What general properties do these estimators have? Explain intuitively why the OLS estimator is identical to the maximum likelihood estimator here. log(2π)- (Requires Appendix material and Calculus)The log of the likelihood function (L)for the simple regression model with i.i.d.normal errors is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum): L = - log(2π)- log σ2 - Derive the maximum likelihood estimator for the slope and intercept.What general properties do these estimators have? Explain intuitively why the OLS estimator is identical to the maximum likelihood estimator here. log σ2 - (Requires Appendix material and Calculus)The log of the likelihood function (L)for the simple regression model with i.i.d.normal errors is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum): L = - log(2π)- log σ2 - Derive the maximum likelihood estimator for the slope and intercept.What general properties do these estimators have? Explain intuitively why the OLS estimator is identical to the maximum likelihood estimator here. Derive the maximum likelihood estimator for the slope and intercept.What general properties do these estimators have? Explain intuitively why the OLS estimator is identical to the maximum likelihood estimator here.

Correct Answer:

verifed

Verified

Maximizing the likelihood function with ...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q13: Nonlinear least squares<br>A)solves the minimization of the

Q19: In the linear probability model, the interpretation

Q20: When having a choice of which estimator

Q24: Equation (11.3)in your textbook presents the regression

Q37: In the expression Pr(deny = 1 <img

Q38: F-statistics computed using maximum likelihood estimators<br>A)cannot be

Q39: In the probit regression,the coefficient β1 indicates<br>A)the

Q41: You have a limited dependent variable (Y)and

Q43: (Requires Appendix material)Briefly describe the difference between

Q43: The major flaw of the linear probability