Multiple Choice
Formulate but do not solve the following exercise as a linear programming problem.
CalJuice Company has decided to introduce three fruit juices made from blending two or more concentrates. These juices will be packaged in 2-qt (64 fluid-oz) cartons. To make one carton of pineapple-orange juice requires 7 oz each of pineapple and orange juice concentrates. To make one carton of orange-banana juice requires 12 oz of orange juice concentrate and 4 oz of banana pulp concentrate. Finally, to make one carton of pineapple-orange-banana juice requires 5 oz of pineapple juice concentrate, 6 oz of orange juice concentrate, and 3 oz of banana pulp. The company has decided to allot 16,000 oz of pineapple juice concentrate, 25,000 oz of orange juice concentrate, and 3,000 oz of banana pulp concentrate for the initial production run. The company also stipulated that the production of pineapple-orange-banana juice should not exceed 500 cartons. Its profit on one carton of pineapple-orange juice is $1.10; its profit on one carton of orange-banana juice is $0.90, and its profit on one carton of pineapple-orange-banana juice is $0.80. To realize a maximum profit, how many cartons of each blend should the company produce?
A) Maximize: 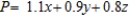
Subject to: 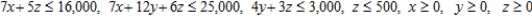
B) Maximize: 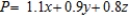
Subject to: 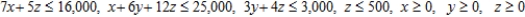
C) Maximize:  Subject to:
Subject to: 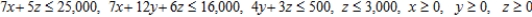
D) Maximize: 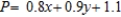
Subject to: 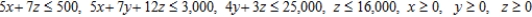
Correct Answer:

Verified
Correct Answer:
Verified
Q14: Kane Manufacturing has a division that produces
Q15: Find the graphical solution of the inequality.
Q16: As a part of a campaign to
Q17: Solve the linear programming problem by the
Q18: Find the optimal (maximum and/or minimum) value(s)
Q20: Find the graphical solution of the inequality.
Q21: A division of the Winston Furniture Company
Q22: Formulate but do not solve the following
Q23: Formulate but do not solve the following
Q24: Formulate but do not solve the following