Multiple Choice
Formulate but do not solve the following exercise as a linear programming problem. Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 4 lb of cast iron and 5 min of labor. To produce each model B grate requires 5 lb of cast iron and 4 min of labor. The profit for each model A grate is $4.00, and the profit for each model B grate is $1.50. If 1,000 lb of cast iron and 25 hr of labor are available for the production of grates per day, how many grates of each model should the division produce per day in order to maximize Kane's profits?
Because of a backlog of orders on model A grates, the manager of Kane Manufacturing has decided to produce at least 150 of these models a day. Operating under this additional constraint, how many grates of each model should Kane produce to maximize profit?
A) Maximize: 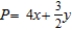 Subject to:
Subject to: 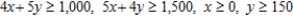
B) Maximize:  Subject to:
Subject to: 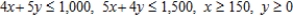
C) Maximize: 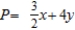 Subject to:
Subject to: 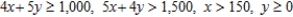
D) Maximize: 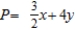 Subject to:
Subject to: 
Correct Answer:

Verified
Correct Answer:
Verified
Q19: Formulate but do not solve the following
Q20: Find the graphical solution of the inequality.
Q21: A division of the Winston Furniture Company
Q22: Formulate but do not solve the following
Q23: Formulate but do not solve the following
Q25: Find the graphical solution of the inequality.
Q26: Find the graphical solution of the inequality.
Q27: Find the optimal (maximum and minimum) values
Q28: A hunger-relief organization, has earmarked between $2
Q29: Perth Mining Company operates two mines for