Multiple Choice
Formulate but do not solve the following exercise as a linear programming problem. A company manufactures products A, B, and C. Each product is processed in three departments: I, II, and III. The total available labor-hours per week for departments I, II, and III are 970, 1,090, and 860, respectively. The time requirements (in hours per unit) and profit per unit for each product are as follows:  How many units of each product should the company produce in order to maximize its profit?
How many units of each product should the company produce in order to maximize its profit?
A) Maximize: 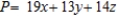 Subject to:
Subject to: 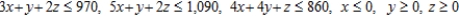
B) Maximize: 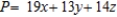 Subject to:
Subject to: 
C) Maximize: 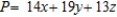 Subject to:
Subject to: 
D) Maximize: 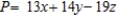 Subject to:
Subject to: 
Correct Answer:

Verified
Correct Answer:
Verified
Q69: Find the graphical solution of the inequality.
Q70: Solve the linear programming problem by the
Q71: Determine graphically the solution set for the
Q72: Solve the linear programming problem by the
Q73: Determine graphically the solution set for the
Q75: Determine graphically the solution set for the
Q76: A veterinarian has been asked to prepare
Q77: Perth Mining Company operates two mines for
Q78: Determine graphically the solution set for the
Q79: Solve the linear programming problem by the