Multiple Choice
Perth Mining Company operates two mines for the purpose of extracting gold and silver. The Saddle Mine costs $16,000/day to operate, and it yields 50 oz of gold and 3,000 oz of silver per day. The Horseshoe Mine costs $17,000/day to operate, and it yields 75 oz of gold and 1,000 ounces of silver each day. Company management has set a target of at least 825 oz of gold and 18,000 oz of silver. How many days should each mine be operated so that the target can be met at a minimum cost? Find the range of values that the cost of operating the Saddle Mine per day can assume without changing the optimal solution.
Find the range of values that the requirement for gold can assume.
Find the shadow price for the requirement for gold.
A) Saddle Mine = 9 days, Horseshoe Mine = 3 days, Minimum cost = $201,000 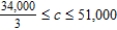
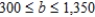 $201,200.00
$201,200.00
B) Saddle Mine = 3 days, Horseshoe Mine = 9 days, Minimum cost = $200,997 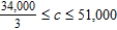
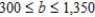 $200.00
$200.00
C) Saddle Mine = 3 days, Horseshoe Mine = 9 days, Minimum cost = $201,007 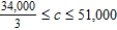
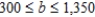
$200.00
D) Saddle Mine = 3 days, Horseshoe Mine = 9 days, Minimum cost = $201,000 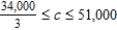
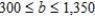 $200.00
$200.00
Correct Answer:

Verified
Correct Answer:
Verified
Q146: Solve the linear programming problem by the
Q147: A veterinarian has been asked to prepare
Q148: Find the graphical solution of the inequality.
Q149: Formulate but do not solve the following
Q150: Soundex produces two models of clock radios.
Q152: Determine graphically the solution set for the
Q153: Use the method of corners to solve
Q154: Write a system of linear inequalities that
Q155: A farmer plans to plant two crops,
Q156: Determine graphically the solution set for the