Ace Novelty Wishes to Produce Two Types of Souvenirs: Type

Short Answer

Ace Novelty wishes to produce two types of souvenirs: type A and type B. Each type-A souvenir will result in a profit of $1.00, and each type-B souvenir will result in a profit of $1.20. To manufacture a type-A souvenir requires 2 minutes on machine I and 1 minute on machine II. A type-B souvenir requires 1 minute on machine I and 3 minutes on machine II. There are 3 hours available on machine I and 5 hours available on machine II for processing the order.
​
Let x be the number of type-A souvenirs and y be the number of type-B souvenirs to be made. Then the problem can be reduced to a linear programming problem with the objective function P = x + 1.2y and constraints
​ ​
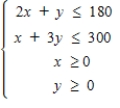
Please enter your answers to two decimal places.
​
Find the contribution to the profit of a type-B souvenir for which the optimal solution holds.
​
$ ≤ c _type-B ≤ $
​
What will be the optimal profit of the company if the contribution to the profit of a type-A souvenir is $1.90 (with the contribution to the profit of a type-B souvenir held at $1.20)?
​
$ __________
​
What will be the optimal profit of the company if the contribution to the profit of a type-B souvenir is $2.80 (with the contribution to the profit of a type-A souvenir held at $1.00)?
​
$ __________