Kane Manufacturing Has a Division That Produces Two Models of Grates

Short Answer

Kane Manufacturing has a division that produces two models of grates, model A and model B. To produce each model A grate requires 3 pounds of cast iron and 6 minutes of labor. To produce each model B grate requires 4 pounds of cast iron and 3 minutes of labor. The profit for each model A grate is $2.00, and the profit for each model B grate is $1.50. Available for grate production each day are 1,160 pounds of cast iron and 22 labor-hours. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 180 grates per day.
​
Let x denote the number of model A grates and y the number of model B grates produced. Then, the problem can be reduced to a linear programming problem with the objective function P = 2x + 1.5y and constraints
​ ​
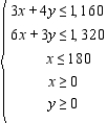
Find the range of values that resource 2 (the constant on the right-hand side of constraint 2) can assume.
​
≤ C _resourse2 ≤
​
By how much can the right-hand side of constraint 3 be decreased so that the current optimal solution still holds?
​
It cannot be decreased by more than __________ units.