Exam 5: Production

Ranger Construction is preparing to repair potholes,under contract to the local county road repair agency.Based on past experience,Ranger has found that output can be described by: Q = K0.5L0.5,where Q = pot holes filled,K = units of capital,and L = units of labor.Ranger can hire labor at $12 per hour,and the cost of capital is $8 per unit.Capacity limitations require that Ranger accepts no more than $96,000 worth of filling this season.What is the optimal mix of inputs for Ranger? How many potholes should Ranger agree to fill? Use the method of Lagrange multipliers to find the solution.

Free

(Essay)

4.7/5

(30)

Question 1

Correct Answer:

Verified

Ranger's objective is: Maximize Q = K^0.⁵L^0.⁵ subject to 8K + 12L = 96,000.
The Lagrange multiplier is: G = K^0.⁵L^0.⁵ + $\lambda$ (8K + 12L - 96,000).The three partial derivatives need to be computed and set equal to zero:
$\partial \mathrm{G}$ / $\partial \mathrm{K}$ = 0.5K^-^0.⁵L^0.⁵+ 8 $\lambda$ = 0 ---- (1)
$\partial \mathrm{G}$ / $\partial \mathrm{L}$ = 0.5K^0.⁵L^-0^.5 + 12 $\lambda$ = 0 ---- (2)
$\partial \mathrm{G}$ / $\partial\lambda$ = 8K + 12L - 96,000 = 0 ---- (3)
Multiply (1)by 1.5:
0.75K^-⁰^.5L^0.⁵ + 12 $\lambda$ = 0 and equate this expression with (2)to get:
0.75K^-⁰^.5L^0.⁵ + 12 $\lambda$ = 0.5K^0.⁵L^-⁰^.5 + 12 $\lambda$
Cancel 12 $\lambda$ ,and then combine terms and simplify:
0.75L = 0.5K,or K = 1.5L
Substitute this last expression into (3):
8(1.5L)+ 12L - 96,000 = 0,or 24L = 96,000
Thus,L = 4,000 units and K = (1.5)(4,000)= 6,000 units.
The firm's level of output is: Q = (6,000)^0.⁵(4,000)^0.⁵ = 4,899 potholes.Ranger should hire 4,000 units of labor,6,000 units of capital,and agree to fill 4,899 potholes.

Carefully define returns to scale,and explain how this differs from marginal returns.

Free

(Essay)

4.8/5

(26)

Question 2

Correct Answer:

Verified

Returns to scale refer to the impact on output if all inputs are changed in the same proportion.For example,if a firm faces constant returns to scale and all inputs increase by 5%,then output will increase by 5%.Marginal returns refer to the impact on output if one input is changed while all other inputs are held fixed.Typically,it is expected that as use of the input increases,the firm will experience diminishing marginal returns.This will be true regardless of returns to scale.Marginal returns to an input applies to the short-run and returns to scale applies in the long-run as all inputs can be varied simultaneously only in the long-run.

Enpar manufactures engine parts for an automotive manufacturer.It operates two plants,A and B,which have the following production functions: QA = 30SA - 0.25SA2 and QB = 40SB - 0.5SB2,where QA and QB denote the outputs of engine parts from each plant and SA and SB denote the amounts of steel used in each plant.Suppose that total steel availability is 40 units.What is the optimal allocation of steel between the two plants?

Free

(Essay)

4.9/5

(34)

Question 3

Correct Answer:

Verified

Enpar maximizes profit when the marginal product for steel is equal at the two plants.
Marginal product of steel at plant A [MP_A] = 30 - 0.5S_A and marginal product of steel at plant B [MP_B] = 40 - S_B.Equating MP_Aand MP_B gives: 30 - 0.5S_A = 40 - S_B.In addition,the availability constraint is: S_A + S_B = 40,so that S_B = 40 - S_A.Substituting this last equation into MP_A = MP_B yields the single equation:
30 - 0.5S_A = 40 - (40 - S_A),so 30 = 1.5S_A.Thus,S_A = 20 and S_B = 20.

Specialty Steel has carefully measured production in its new plant to determine whether it is technically efficient in production.It has found that,for its two inputs K and L,it has the following marginal products: MPK = 15 units and MPL = 22 units.The inputs are hired in perfectly competitive markets,and the firm faces input costs of PK = $7.50 and PL = $10 per unit. You have been hired as a consultant to assist Specialty in increasing profitability.What do you recommend about production planning? Explain.

(Essay)

4.8/5

(30)

Question 4

The following table shows the total output produced in a factory at various levels of employment of labor.The firm sells each unit of output at $2 and each worker is paid a wage of $32. Table 5-1 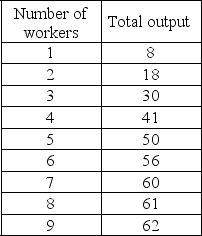-Refer to Table 5-1.What is the marginal revenue associated with the 2nd worker?

(Multiple Choice)

4.9/5

(33)

Question 5

The following table shows the total output produced in a factory at various levels of employment of labor.The firm sells each unit of output at $2 and each worker is paid a wage of $32. Table 5-1 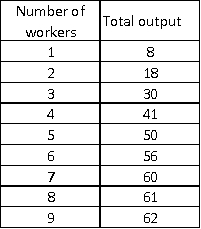-Refer to Table 5-1.Diminishing returns to labor occurs beyond _____ workers.

(Multiple Choice)

4.8/5

(35)

Question 6

Sleak Teak builds yard furniture,using domestic hardwoods and (in a smaller shop)handcrafted knick-knacks from the same sort of wood.Although hardwoods were readily available in the past,recently they have been much more difficult to obtain.Consultation with the plant managers of the two lines has resulted in the following production functions for hardwood usage in the two products: Yard furniture: Y = 2T_Y - 0.001T_Y² Knick-knack: K = 20T_K - 0.01T_K², where Y and K denote units of the two types of products and T_Y and T_K denote teak used in yard furniture and knick-knacks respectively.Yard furniture can be sold at a profit of $100 per unit,and knick-knacks can be sold at a profit of $25 each.Sleak Teak has 1,300 units of teak available.How should it be allocated across the two products? Explain.

(Essay)

4.9/5

(35)

Question 7

A profit-maximizing firm will hire the variable input,labor,until the point where:

(Multiple Choice)

4.9/5

(40)

Question 8

What does the law of diminishing marginal returns state?

(Multiple Choice)

4.8/5

(36)

Question 9

Which of the following identifies the optimal usage of inputs by a profit-maximizing firm?

(Multiple Choice)

4.8/5

(38)

Question 10

Which of the following correctly defines the marginal product of labor?

(Multiple Choice)

4.8/5

(41)

Question 11

If there is a change in input prices,what is the most likely impact on production isoquants?

(Multiple Choice)

5.0/5

(31)

Question 12

When the marginal product of a variable input is zero,it implies that the firm is at the point where the total product is:

(Multiple Choice)

4.9/5

(31)

Question 13

The marginal revenue product of labor [MRPL] is equal to the product of:

(Multiple Choice)

4.8/5

(31)

Question 14

If the sum of the exponents of a Cobb-Douglas production function is equal to 1.2,the production function exhibits:

(Multiple Choice)

4.8/5

(35)

Question 15

The marginal product of labor initially rises as more labor is employed because of:

(Multiple Choice)

4.8/5

(33)

Question 16

The following table shows the total output produced in a factory at various levels of employment of labor.The firm sells each unit of output at $2 and each worker is paid a wage of $32. Table 5-1 -Refer to Table 5-1.What is the marginal revenue product of the 4th worker?

(Multiple Choice)

4.8/5

(36)

Question 17

Which of the following is true of a firm that faces increasing returns to scale?

(Multiple Choice)

4.8/5

(34)

Question 18

Assume that a firm employs labor and capital by paying $40 per unit of labor employed and $200 per hour to rent a unit of capital.Given that the production function is given by: Q = 10L - L2 + 60K -1.5K2,where Q is total output,L is labor,and K is capital,what is the firm's optimal combination of capital and labor?

(Essay)

4.7/5

(42)

Question 19

The following table shows the total output produced in a factory at various levels of employment of labor.The firm sells each unit of output at $2 and each worker is paid a wage of $32. Table 5-1 -Refer to Table 5-1.When the firm employs _____ workers,marginal profit per unit of output is at its maximum.

(Multiple Choice)

4.8/5

(25)

Question 20

Showing 1 - 20 of 51

Carefully define returns to scale,and explain how this differs from marginal returns.

The following table shows the total output produced in a factory at various levels of employment of labor.The firm sells each unit of output at $2 and each worker is paid a wage of $32. Table 5-1 -Refer to Table 5-1.What is the marginal revenue associated with the 2nd worker?

The following table shows the total output produced in a factory at various levels of employment of labor.The firm sells each unit of output at $2 and each worker is paid a wage of $32. Table 5-1 -Refer to Table 5-1.Diminishing returns to labor occurs beyond _____ workers.

A profit-maximizing firm will hire the variable input,labor,until the point where:

What does the law of diminishing marginal returns state?

Which of the following identifies the optimal usage of inputs by a profit-maximizing firm?

Which of the following correctly defines the marginal product of labor?

If there is a change in input prices,what is the most likely impact on production isoquants?

When the marginal product of a variable input is zero,it implies that the firm is at the point where the total product is:

The marginal revenue product of labor [MRPL] is equal to the product of:

If the sum of the exponents of a Cobb-Douglas production function is equal to 1.2,the production function exhibits:

The marginal product of labor initially rises as more labor is employed because of:

The following table shows the total output produced in a factory at various levels of employment of labor.The firm sells each unit of output at $2 and each worker is paid a wage of $32. Table 5-1 -Refer to Table 5-1.What is the marginal revenue product of the 4th worker?

Which of the following is true of a firm that faces increasing returns to scale?

Introduction to Economic Decision Making

Optimal Decisions Using Marginal Analysis

Demand Analysis and Optimal Pricing

Estimating and Forecasting Demand

Cost Analysis

Perfect Competition

Monopoly

Oligopoly

Game Theory and Competitive Strategy

Regulation, Public Goods, and Benefit-Cost Analysis

Decision Making Under Uncertainty

The Value of Information

Asymmetric Information and Organizational Design

Bargaining and Negotiation

Auctions and Competitive Bidding

Linear Programming

Filters