Exam 5: Uncertainty and Consumer Behavior

Assume that one of two possible outcomes will follow a decision.One outcome yields a $75 payoff and has a probability of 0.3; the other outcome has a $125 payoff and has a probability of 0.7.In this case the expected value is

Free

(Multiple Choice)

4.9/5

(36)

Question 1

Correct Answer:

Verified

Connie's utility depends upon her income.Her utility function is U = I^1/2.She has received a prize that depends on the roll of a pair of dice.If she rolls a 3,4,6 or 8,she will receive $400.Otherwise she will receive $100. a.What is the expected payoff from this prize? [Hint: The probability of rolling a 3 is 1/18,the probability of rolling a 4 is 3/36,the probability of rolling a 6 is 5/36,and the probability of rolling an 8 is 5/36] b.What is the expected utility from this prize? c.Connie is offered an alternate prize of $169 (no dice roll is required).Will she accept the alternate prize or roll the dice? d.What is the minimum payment that Connie will accept to forego the roll of the dice?

Free

(Essay)

4.8/5

(33)

Question 2

Correct Answer:

Verified

Expected return on stock: a. The probability of receiving $400 is 5/12.The probability of receiving $100 is 7/12. Expected payoff = ($400)(5/12)+ ($100)(7/12) = $166.67 + $58.33 = $225 b. The utility from $400 is (400)^1/2 = 20 utils.The utility from $100 is (100)^1/2 = 10 utils. Expected utility = (20 utils)(5/12)+ (10 utils)(7/12) = 8.33 utils + 5.83 utils = 14.16 utils c. The utility from $169 is (169)^1/2 = 13 utils.The utility from rolling the dice (14.16 utils)is greater than the utility from a certain $169,therefore,Connie will turn down the $169 alternative prize and roll the dice. d. To convince Connie to accept a cash payment in lieu of rolling the dice the cash payment will have to provide more utility than rolling the dice.The expected utility from rolling the dice is 14.16 utils (see 1b).The cash payment that will yield 14.16 utils is calculated as follows: 14.16 = I^1/2 14.16² = I 200.51 = I Connie is indifferent between a cash payment or $200.51 and a roll of the dice.A payment of $200.52 is preferred to the roll of the dice.

The information in the table below describes choices for a new doctor.The outcomes represent different macroeconomic environments,which the individual cannot predict. Table 5.3 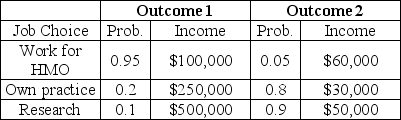-Refer to Table 5.3.The expected returns are highest for the physician who

Free

(Multiple Choice)

4.9/5

(35)

Question 3

Correct Answer:

Verified

Individuals who fully insure their house and belongings against fire

(Multiple Choice)

4.9/5

(39)

Question 4

Upon graduation,you are offered three jobs. 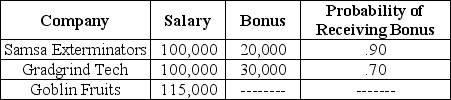Rank the three job offers in terms of expected income,from the highest to the lowest.

(Multiple Choice)

4.7/5

(33)

Question 5

Table 5.4 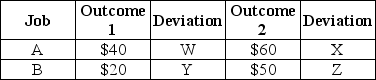-Refer to Table 5.4.If outcomes 1 and 2 are equally likely at Job A,then the standard deviation of payoffs at Job A is

(Multiple Choice)

4.7/5

(30)

Question 6

Marsha owns a boat that is harbored on the east coast of the United States.Currently,there is a hurricane that is approaching her harbor.If the hurricane strikes her harbor,her wealth will be diminished by the value of her boat,as it will be destroyed.The value of her boat is $250,000.It would cost Marsha $15,000 to move the boat to a harbor out of the path of the hurricane.Marsha's utility of wealth function is 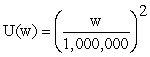. Marsha's current wealth is $3 million including the value of the boat.Past evidence has influenced Marsha to believe that the hurricane will likely miss her harbor,and so she plans not to move her boat.Suppose the probability the hurricane will strike Marsha's harbor is 0.7.Calculate Marsha's expected utility given that she will not move her boat.Calculate Marsha's expected utility if she moves her boat.Which of the two options gives Marsha the highest expected utility?

(Essay)

4.8/5

(38)

Question 7

Consider the following statements when answering this question; I.The allocation of a risk averse investor's portfolio between a risk free asset and a risky asset never changes if the rate of return on both assets increases by the same amount. II.Given the choice between investing in a risk free asset or a risky asset with higher expected returns,the utility maximizing portfolio of a risk neutral or risk loving investor would never include the risk free asset.

(Multiple Choice)

4.8/5

(38)

Question 8

How might department stores best protect themselves against the risk of recession?

(Multiple Choice)

4.8/5

(39)

Question 9

Blanca has her choice of either a certain income of $20,000 or a gamble with a 0.5 probability of $10,000 and a 0.5 probability of $30,000.The expected value of the gamble:

(Multiple Choice)

4.9/5

(26)

Question 10

Assume that two investment opportunities have identical expected values of $100,000.Investment A has a variance of 25,000,while investment B's variance is 10,000.We would expect most investors (who dislike risk)to prefer investment opportunity

(Multiple Choice)

4.7/5

(35)

Question 11

The expected value of a project is always the

(Multiple Choice)

4.7/5

(40)

Question 12

An investment opportunity has two possible outcomes,and the value of the investment opportunity is $250.One outcome yields a $100 payoff and has a probability of 0.25.What is the probability of the other outcome?

(Multiple Choice)

4.8/5

(30)

Question 13

The tendency for individuals to assign higher values to goods when they own the goods than when they do not possess the goods is known as the:

(Multiple Choice)

4.8/5

(32)

Question 14

Behavioral economists argue that asset price bubbles and other examples of herd behavior may be due to biases resulting from the law of small numbers.In particular,the investors may observe unusually returns for some asset and use this limited information to the probability that returns will be high in the future.

(Multiple Choice)

4.9/5

(31)

Question 15

Table 5.4 -Refer to Table 5.4.If at Job B the $20 outcome occurs with probability .2,and the $50 outcome occurs with probability .8,then the standard deviation of payoffs at Job B is nearest which value?

(Multiple Choice)

4.9/5

(31)

Question 16

Nervous Norman holds 70% of his assets in cash,earning 0%,and 30% of his assets in an insured savings account,earning 2%.The expected return on his portfolio

(Multiple Choice)

4.9/5

(36)

Question 17

A farmer lives on a flat plain next to a river.In addition to the farm,which is worth $F,the farmer owns financial assets worth $A.The river bursts its banks and floods the plain with probability P,destroying the farm.If the farmer is risk averse,then the willingness to pay for flood insurance unambiguously falls when

(Multiple Choice)

4.8/5

(26)

Question 18

Sandra lives in the Pacific Northwest and enjoys walking to and from work during sunny days.Her utility is sharply diminished if she must walk while it is raining.Sandra's utility function is U = 1,000 I₁ + 250 I₂ + 1 I₃ where I₁ = 1 if she walks and there is no rain and I₁ = 0 otherwise,I₂ = 1 if she drives to work and I₂ = 0 otherwise,and I₃ = 1 if she walks and it rains and I₃ = 0 otherwise.Sandra believes that the probability of rain today is ³/₁₀.Given her beliefs,what is her expected utility from walking to work? What is her expected utility from driving to work according to her beliefs? If Sandra maximizes her expected utility according to her beliefs,will she drive or walk to work? Sandra missed the weather report this morning that stated the true probability of rain today is ⁴/₅.Given the weather report is accurate,what is Sandra's true expected utility from walking and driving to work? How much could Sandra increase her expected utility if she read and believed the weather report?

(Essay)

4.9/5

(33)

Question 19

Donna is considering the option of becoming a co-owner in a business.Her investment choices are to hold a risk free asset that has a return of R_jand co-ownership of the business,which has a rate of return of R_band a level of risk of σ_b.Donna's marginal rate of substitution of return for risk 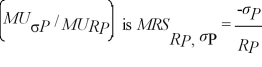where R_Pis Donna's portfolio rate of return and σ_Pis her optimal portfolio risk.Donna's budget constraint is given by 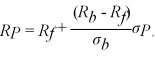Solve for Donna's optimal portfolio rate of return and risk as a function of R_j_, R_b_,_andσ_b.Suppose the table below lists the relevant rates of returns and risks.Use this table to determine Donna's optimal rate or return and risk. Investment Rate of Return Risk Risk Free 0.06 0 Business 0.25 0.39

(Essay)

4.8/5

(32)

Question 20

Showing 1 - 20 of 144

Assume that one of two possible outcomes will follow a decision.One outcome yields a $75 payoff and has a probability of 0.3; the other outcome has a $125 payoff and has a probability of 0.7.In this case the expected value is

The information in the table below describes choices for a new doctor.The outcomes represent different macroeconomic environments,which the individual cannot predict. Table 5.3 -Refer to Table 5.3.The expected returns are highest for the physician who

Individuals who fully insure their house and belongings against fire

Upon graduation,you are offered three jobs. Rank the three job offers in terms of expected income,from the highest to the lowest.

Table 5.4 -Refer to Table 5.4.If outcomes 1 and 2 are equally likely at Job A,then the standard deviation of payoffs at Job A is

How might department stores best protect themselves against the risk of recession?

Blanca has her choice of either a certain income of $20,000 or a gamble with a 0.5 probability of $10,000 and a 0.5 probability of $30,000.The expected value of the gamble:

Assume that two investment opportunities have identical expected values of $100,000.Investment A has a variance of 25,000,while investment B's variance is 10,000.We would expect most investors (who dislike risk)to prefer investment opportunity

The expected value of a project is always the

An investment opportunity has two possible outcomes,and the value of the investment opportunity is $250.One outcome yields a $100 payoff and has a probability of 0.25.What is the probability of the other outcome?

The tendency for individuals to assign higher values to goods when they own the goods than when they do not possess the goods is known as the:

Table 5.4 -Refer to Table 5.4.If at Job B the $20 outcome occurs with probability .2,and the $50 outcome occurs with probability .8,then the standard deviation of payoffs at Job B is nearest which value?

Nervous Norman holds 70% of his assets in cash,earning 0%,and 30% of his assets in an insured savings account,earning 2%.The expected return on his portfolio

Preliminaries

The Basics of Supply and Demand

Consumer Behavior

Individual and Market Demand

Production

The Cost of Production

Profit Maximization and Competitive Supply

The Analysis of Competitive Markets

Market Power: Monopoly and Monopsony

Pricing With Market Power

Monopolistic Competition and Oligopoly

Game Theory and Competitive Strategy

Markets for Factor Inputs

Investment,time and Capital Markets

General Equilibrium and Economic Efficiency 1-83

Markets With Asymmetric Information

Externalities and Public Goods

Filters