Exam 6: Differential Equations
Exam 1: Preparation for Calculus96 Questions
Exam 2: Limits and Their Properties119 Questions
Exam 3: Differentiation208 Questions
Exam 4: Applications of Differentiation147 Questions
Exam 5: Integration165 Questions
Exam 6: Differential Equations88 Questions
Exam 7: Applications of Integration90 Questions
Exam 8: Integration Techniques, L'Hôpital's Rule, and Improper Integrals142 Questions
Exam 9: Infinite Series199 Questions
Exam 10: Parametric Equations, Polar Coordinates, and Vectors173 Questions
Exam 11: Mechanical Ventilation and Sedation: Assessment, Medications, and Complications225 Questions
Select questions type
The logistic function 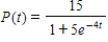 models the growth of a population.Determine when the population reaches 40% of the maximum carrying capacity.Round your answer to three decimal places.
models the growth of a population.Determine when the population reaches 40% of the maximum carrying capacity.Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (39)
(39)
Determine whether the function 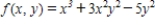 is homogeneous and determine its degree if it is.
is homogeneous and determine its degree if it is.
(Multiple Choice)
4.9/5  (34)
(34)
Consider the differential equation 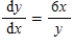 ,for
,for 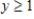 only,with initial value
only,with initial value 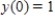 .
Using Euler's Method with step size
.
Using Euler's Method with step size 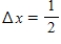 ,what is the estimate for
,what is the estimate for 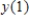 ?
?
(Multiple Choice)
4.9/5  (38)
(38)
Select from the choices below the slope field for the differential equation. 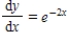
(Multiple Choice)
4.9/5  (43)
(43)
Find the exponential function 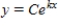 that passes through the two given points.Round your values of C and k to four decimal places.
that passes through the two given points.Round your values of C and k to four decimal places. 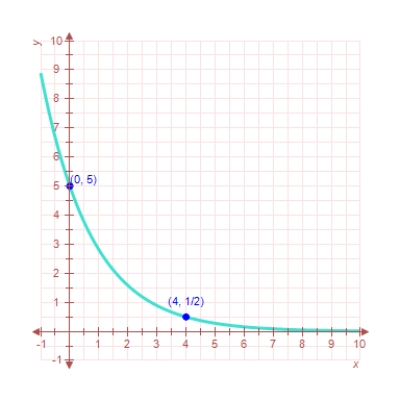
(Multiple Choice)
4.7/5  (43)
(43)
Write and solve the differential equation that models the following verbal statement.Evaluate the solution at the specified value of the independent variable,rounding your answer to four decimal places:
The rate of change of N is proportional to N.When 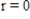 ,
, 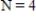 and when
and when 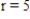 ,
, 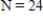 .What is the value of N when
.What is the value of N when 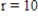 ?
?
(Multiple Choice)
4.8/5  (42)
(42)
Use integration to find a general solution of the differential equation. 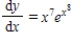
(Multiple Choice)
4.7/5  (43)
(43)
Select from the choices below the slope field for the differential equation. 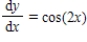
(Multiple Choice)
4.7/5  (46)
(46)
Find the time (in years)necessary for 1,000 to double if it is invested at a rate 6% compounded continuously.Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (26)
(26)
The half-life of the radium isotope Ra-226 is approximately 1,599 years.What percent of a given amount remains after 100 years? Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (31)
(31)
At time 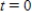 minutes,the temperature of an object is
minutes,the temperature of an object is 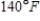 .The temperature of the object is changing at the rate given by the differential equation
.The temperature of the object is changing at the rate given by the differential equation 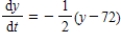 .Use Euler's Method to approximate the particular solutions of this differential equation at
.Use Euler's Method to approximate the particular solutions of this differential equation at 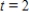 .Use a step size of
.Use a step size of 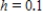 .Round your answer to one decimal place.
.Round your answer to one decimal place.
(Multiple Choice)
4.8/5  (37)
(37)
A population of rabbits in a certain habitat grows according to the differential equation 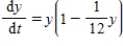 where t is measured in months
where t is measured in months 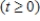 and y is measured in hundreds of rabbits.There were initially 100 rabbits in this habitat;that is,
and y is measured in hundreds of rabbits.There were initially 100 rabbits in this habitat;that is, 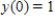 .
Estimates of y(t)can be produced using Euler's Method with step size
.
Estimates of y(t)can be produced using Euler's Method with step size 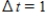 .To the nearest rabbit,the estimate for y(2)is
.To the nearest rabbit,the estimate for y(2)is
(Multiple Choice)
4.7/5  (40)
(40)
Suppose that the population (in millions)of Hungary in 2007 was 10 and that the expected continuous annual rate of change of the population is -0.003.Find the exponential growth model 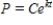 for the population by letting
for the population by letting 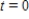 correspond to 2000.Round your answer to four decimal places.
correspond to 2000.Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (40)
(40)
Showing 21 - 40 of 88
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)