Exam 6: Differential Equations
Exam 1: Preparation for Calculus96 Questions
Exam 2: Limits and Their Properties119 Questions
Exam 3: Differentiation208 Questions
Exam 4: Applications of Differentiation147 Questions
Exam 5: Integration165 Questions
Exam 6: Differential Equations88 Questions
Exam 7: Applications of Integration90 Questions
Exam 8: Integration Techniques, L'Hôpital's Rule, and Improper Integrals142 Questions
Exam 9: Infinite Series199 Questions
Exam 10: Parametric Equations, Polar Coordinates, and Vectors173 Questions
Exam 11: Mechanical Ventilation and Sedation: Assessment, Medications, and Complications225 Questions
Select questions type
Use Euler's Method to make a table of values for the approximate solution of the following differential equation with specified initial value.Use 5 steps of size 0.15. 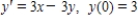
(Multiple Choice)
4.8/5  (32)
(32)
Match the logistic equation and initial condition with the graph of the solution. 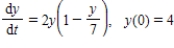
(Multiple Choice)
4.9/5  (33)
(33)
Which of the following is a solution of the differential equation 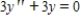 ?
?
(Multiple Choice)
4.8/5  (19)
(19)
Use integration to find a general solution of the differential equation 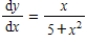 .
.
(Multiple Choice)
4.9/5  (37)
(37)
Find an equation of the graph that passes through the point (2,5)and has the slope 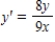 .
.
(Multiple Choice)
4.9/5  (33)
(33)
Sketch the slope field for the differential equation 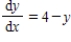 and use the slope field to sketch the solution satisfying the condition
and use the slope field to sketch the solution satisfying the condition 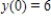 .
.
(Multiple Choice)
4.8/5  (36)
(36)
Write and solve the differential equation that models the following verbal statement:
The rate of change of M with respect to s is proportional to 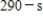 .
.
(Multiple Choice)
4.8/5  (25)
(25)
Which of the following is a solution of the differential equation 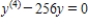 ?
?
(Multiple Choice)
4.8/5  (41)
(41)
Water flows continuously from a large tank at a rate proportional to the amount of water remaining in the tank;that is, 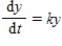 .There was initially 9,000 cubic feet of water in the tank,and at time
.There was initially 9,000 cubic feet of water in the tank,and at time 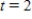 hours,8,000 cubic feet of water remained.
What is the value of k in the equation
hours,8,000 cubic feet of water remained.
What is the value of k in the equation 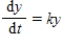 ? Round your answer to 3 decimal places.
? Round your answer to 3 decimal places.
(Multiple Choice)
4.8/5  (29)
(29)
The logistic function 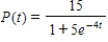 models the growth of a population.Identify the maximum carrying capacity.
models the growth of a population.Identify the maximum carrying capacity.
(Multiple Choice)
4.9/5  (34)
(34)
The isotope 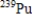 has a half-life of 24,100 years.After 1,000 years,a sample of the isotope is reduced to 1.4 grams.What was the initial size of the sample (in grams)? How much will remain after 10,000 years (i.e. ,after another 9,000 years)? Round your answers to four decimal places.
has a half-life of 24,100 years.After 1,000 years,a sample of the isotope is reduced to 1.4 grams.What was the initial size of the sample (in grams)? How much will remain after 10,000 years (i.e. ,after another 9,000 years)? Round your answers to four decimal places.
(Multiple Choice)
4.9/5  (33)
(33)
Use integration to find a general solution of the differential equation 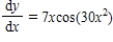
(Multiple Choice)
4.9/5  (32)
(32)
Each of the following graphs is from a logistic function 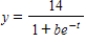 .Which one has the largest value of b?
.Which one has the largest value of b?
(Multiple Choice)
4.8/5  (36)
(36)
The isotope 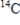 has a half-life of 5,715 years.After 20,000 years,a sample of the isotope is reduced 0.7 grams.What was the initial size of the sample (in grams)? How large was the sample after the first 2,000 years? Round your answers to four decimal places.
has a half-life of 5,715 years.After 20,000 years,a sample of the isotope is reduced 0.7 grams.What was the initial size of the sample (in grams)? How large was the sample after the first 2,000 years? Round your answers to four decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
Use integration to find a general solution of the differential equation . 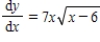
(Multiple Choice)
4.8/5  (43)
(43)
The rate of change of N is proportional to N.When 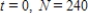 and when
and when 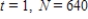 .What is the value of N when
.What is the value of N when 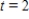 ? Round your answer to three decimal places.
? Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (37)
(37)
Use integration to find a general solution of the differential equation. 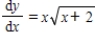
(Multiple Choice)
4.7/5  (27)
(27)
Showing 61 - 80 of 88
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)