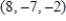Exam 16: The Nature of Mathematical Systems
Exam 1: The Nature of Problem Solving53 Questions
Exam 2: The Nature of Sets64 Questions
Exam 3: The Nature of Logic160 Questions
Exam 4: The Nature of Numeration Systems102 Questions
Exam 5: The Nature of Numbers139 Questions
Exam 6: The Nature of Algebra173 Questions
Exam 7: The Nature of Geometry139 Questions
Exam 8: The Nature of Measurement50 Questions
Exam 9: The Nature of Networks and Graph Theory76 Questions
Exam 10: The Nature of Growth57 Questions
Exam 11: The Nature of Sequences, Series, and Financial Management130 Questions
Exam 12: The Nature of Counting78 Questions
Exam 13: The Nature of Probability97 Questions
Exam 14: The Nature of Statistics82 Questions
Exam 15: The Nature of Graphs and Functions74 Questions
Exam 16: The Nature of Mathematical Systems97 Questions
Exam 17: The Nature of Voting and Apportionment52 Questions
Select questions type
Solve the system by the addition method. 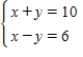
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
A
An after-shave lotion is 50% alcohol. If you have 4 fluid ounces of the lotion, how much water must be added to reduce the mixture to 10% alcohol?
Free
(Multiple Choice)
4.8/5  (42)
(42)
Correct Answer:
B
Given the matrix, perform elementary row operation to obtain a 1 in the row 1, column 1 position.
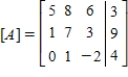
(Short Answer)
4.8/5  (40)
(40)
An after-shave lotion is 40% alcohol. If you have 15 fluid ounces of the lotion, how much water must be added to reduce the mixture to 30% alcohol?
__________ ounces of water
(Short Answer)
4.8/5  (42)
(42)
Decide which of the points below is a feasible solution for the given constraints. 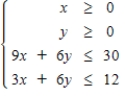
(Multiple Choice)
5.0/5  (43)
(43)
The Thompson Company manufactures two industrial products, standard ($55 profit per item) and economy ($25 profit per item). These items are built using machine time and manual labor. The standard product requires 4 hr of machine time and 3 hr of manual labor. The economy model requires 4 hr of machine time and no manual labor. If the week's supply of manual labor is limited to 600 hr and machine time to 12,000 hr, how much of each type of product should be produced each week to maximize the profit?
__________ standard models and __________ economy models.
(Essay)
4.8/5  (43)
(43)
If row 7 of a matrix [A] is multiplied by 4 and then added to row 4 of [A], then the correct notation is *Row (4,[A],7,4). Decide whether the statement is true or false.
(True/False)
4.8/5  (42)
(42)
If row 5 of a matrix [C] is multiplied by -3 and then added to row 6 of [C], then the correct notation is Row+(-3,[C],6,5). Decide whether the statement is true or false.
(True/False)
4.7/5  (32)
(32)
A collection of coins has a value of $4.12. There is the same number of nickels and dimes but four fewer pennies than nickels or dimes. How many pennies are in the collection if there are 74 coins?
(Multiple Choice)
4.8/5  (33)
(33)
A plane with a tail wind makes its 1,440-mile flight in 4 hours. The return flight against the wind takes a half hour longer. What is the wind speed? Round to one decimal place, if required.
__________ mph
(Short Answer)
4.9/5  (37)
(37)
The Thompson Company manufactures two industrial products, standard ($45 profit per item) and economy ($30 profit per item). These items are built using machine time and manual labor. The standard product requires 2 hr of machine time and 1 hr of manual labor. The economy model requires 2 hr of machine time and no manual labor. If the week's supply of manual labor is limited to 900 hr and machine time to 9,000 hr, how much of each type of product should be produced each week to maximize the profit?
(Multiple Choice)
4.9/5  (33)
(33)
Write a linear programming model, including the objective function and the set of constraints for the following problem. DO NOT SOLVE, but be sure to define all your variables.
Brown Bros., Inc., is an investment company doing an analysis of the pension fund for a certain company. The fund has a maximum of $10 million to invest in two places: no more than $8 million in stocks yielding 12%, and at least $2 million in long-term bonds yielding 9%. The stock-to-bond investment ratio cannot be more than 2 to 1. How should Brown Bros. advise its client so that the investments yield the maximum yearly return?
DENOTE:
X = amount invested in stock (in millions of dollars)
Y = amount invested in bonds (in millions of dollars)
(Multiple Choice)
4.9/5  (37)
(37)
Solve the system by solving the corresponding matrix equation with an inverse. 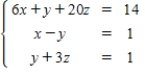
(Multiple Choice)
4.8/5  (42)
(42)
Showing 1 - 20 of 97
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)