Exam 7: Production Cost: Many Variable Inputs
Exam 1: Microeconomics: a Working Methodology98 Questions
Exam 2: A Theory of Preferences103 Questions
Exam 3: Demand Theory93 Questions
Exam 4: More Demand Theory94 Questions
Exam 5: Intertemporal Decision Making and Capital Values94 Questions
Exam 6: Production Cost: One Variable Input94 Questions
Exam 7: Production Cost: Many Variable Inputs96 Questions
Exam 8: The Theory of Perfect Competition102 Questions
Exam 9: Applications of the Competitive Model96 Questions
Exam 10: Monopoly99 Questions
Exam 11: Input Markets and the Allocation of Resources98 Questions
Exam 12: Labour Market Applications80 Questions
Exam 13: Competitive General Equilibrium95 Questions
Exam 14: Price Discrimination Monopoly Practices94 Questions
Exam 15: Introduction to Game Theory83 Questions
Exam 16: Game Theory and Oligopoly90 Questions
Exam 17: Choice Making Under Uncertainty86 Questions
Exam 18: Assymmetric Information, the Rules of the Game, and Externalities98 Questions
Exam 19: The Theory of the Firm96 Questions
Exam 20: Assymetric Information and Market Behaviour101 Questions
Select questions type
When returns to scale are constant, long run marginal cost is:
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
D
Interior solutions of the cost minimizing problem, given convex isoquants, are characterized by:
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
Coal- fired steam locomotives become more efficient for railroads relative to oil- burning diesel locomotives as:
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
A
A firm has the following long- run production function y = z11/2z21/2
where z1 and z2 are the two inputs used in production and y is the output. Let w1 and w2 be the input prices.
i)What is the returns to scale of this production function?
ii)Assume both inputs are variable and the input prices are w1 = 4 and w2 = 9. The firm minimizes cost. Derive the conditional input demand functions.
iii)Derive an equation for the output expansion path.
iv)Find the firm's long- run total cost function.
(Essay)
4.7/5  (37)
(37)
Suppose MTRS =MPL/MPK=1/3. If we want to reduce K by 6 units and keep output constant, we have to increase L by units.
(Multiple Choice)
4.8/5  (34)
(34)
The firm has a production function given by f(L,K)= L1/4K1/2. Currently, the wage rate is 9 and the rental rate of capital is 2 and this firm has a contract to produce 24 units of output. How much labour and capital will this firm hire?
(Essay)
4.8/5  (39)
(39)
A lawn care service has a production function given by f(L,K)= min(4L,5K). If the price of L
is 8 and the price of K is 5, what is its marginal cost for caring for an additional yard?
(Essay)
4.8/5  (25)
(25)
Herongate Horses produces saddles (y)using two inputs, leather (z1)and labour (z2). Herongate Horses' production function is given by: F(z1, z2)= (1/4)z1z2
i)Does Herongate Horses' production function exhibit constant, increasing, or decreasing returns to scale?
ii)Graph Herongate Horses' isoquant for y = 4. Calculate the slope of the isoquant as a function of z1 and z2.
iii)Calculate Herongate Horses' conditional input demands for z1 and z2 as a function of y, when w1 = 5 and
w2 = 20.
iv)Using your answer to (iii), find Herongate Horses' total cost function. Graph the total cost function, TC(y). Find and graph the long run average cost function, LAC(y).
(Essay)
4.9/5  (29)
(29)
Competitive firms are most likely to exist when average cost curves:
(Multiple Choice)
4.8/5  (35)
(35)
If isoquants are smooth and convex, then a necessary condition for cost minimization is that the:
(Multiple Choice)
4.9/5  (28)
(28)
If an industry is characterized by universal constant returns to scale:
(Multiple Choice)
4.7/5  (25)
(25)
Figure 7A
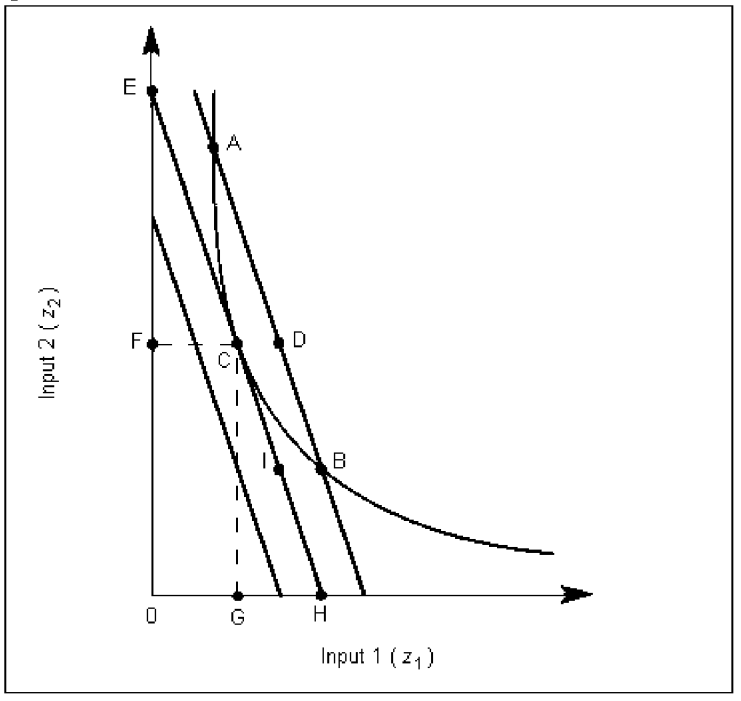 -The optimum quantity of output in Figure 7A is given by the line:
-The optimum quantity of output in Figure 7A is given by the line:
(Multiple Choice)
4.8/5  (32)
(32)
Showing 1 - 20 of 96
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)