Exam 13: Modeling Computation
Exam 1: The Foundations: Logic and Proofs200 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices214 Questions
Exam 3: Algorithms52 Questions
Exam 4: Number Theory and Cryptography154 Questions
Exam 5: Induction and Recursion53 Questions
Exam 6: Counting156 Questions
Exam 7: Discrete Probability53 Questions
Exam 8: Advanced Counting Techniques128 Questions
Exam 9: Relations74 Questions
Exam 10: Graphs127 Questions
Exam 11: Trees97 Questions
Exam 12: Boolean Algebra77 Questions
Exam 13: Modeling Computation71 Questions
Select questions type
Suppose a phrase-structure grammar has productions
Find a derivation of 010 .
(Short Answer)
4.9/5  (31)
(31)
Suppose a phrase-structure grammar has productions Finf a derivation of 01 .
(Short Answer)
4.8/5  (34)
(34)
Suppose a phrase-structure grammar has productions Find a derivation of 1000 .
(Short Answer)
4.8/5  (37)
(37)
For the following Turing machines T, find the final tape when T is run on the following tape, beginning in the
initial position (the first nonzero entry from the left): \@cdots 0 0 0 1 0 \@cdots
(Short Answer)
4.9/5  (34)
(34)
For the following Turing machine T, find the final tape when T is run on the following tape, beginning in the
initial position (the first nonzero entry from the left): \@cdots 0 0 0 1 0 \@cdots ,0,,1,R , ,1,,1,L , ,0,,1,L
(Short Answer)
4.8/5  (33)
(33)
Construct a finite-state machine that models a vending machine accepting only quarters that gives a container
of orange juice when 50 cents has been deposited, followed by a button being pushed. (The possible inputs
are quarters and the button, and the possible outputs are nothing, orange juice, and a quarter. The machine
returns any extra quarters.)
(Short Answer)
4.9/5  (39)
(39)
Suppose a phrase-structure grammar has productions Find a derivation of 0011 .
(Short Answer)
4.8/5  (29)
(29)
Find all strings recognized by this deterministic finite-state automaton. 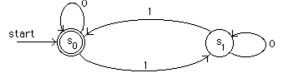
(Short Answer)
5.0/5  (38)
(38)
Which strings are recognized by the following finite-state automaton? 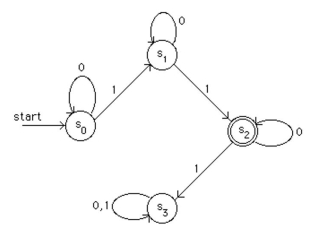
(Short Answer)
4.8/5  (40)
(40)
Suppose a phrase-structure grammar has productions Find a derivation of 0100 .
(Short Answer)
4.8/5  (41)
(41)
For the following Turing machine T, find the final tape when T is run on the following tape, beginning in the
initial position (the first nonzero entry from the left): \@cdots 0 0 0 1 0 \@cdots
(Short Answer)
4.9/5  (38)
(38)
In questions determine the output for
- each input string, using this state table. 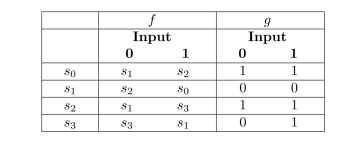
(Short Answer)
4.7/5  (34)
(34)
Suppose a phrase-structure grammar has productions
Find a derivation of 110000 .
(Short Answer)
4.7/5  (31)
(31)
Showing 21 - 40 of 71
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)