Exam 4: Polynomial and Rational Functions
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Provide an appropriate response.
-What are the possible numbers of real zeros (counting multiplicities) for a polynomial function with real coefficients of degree six?
(Multiple Choice)
4.8/5  (38)
(38)
Use the factor theorem to decide whether or not the second polynomial is a factor of the first.
-
(Multiple Choice)
4.8/5  (34)
(34)
Round to the nearest tenth unless indicated otherwise.
-The force needed to keep a car from skidding on a curve varies jointly as the weight of the car and the square of the car's speed, and inversely as the radius of the curve. If a force of 3600 pounds is
Needed to keep an 1800 pound car traveling at 20 mph from skidding on a curve of radius 600 feet,
What force would be required to keep the same car from skidding on a curve of radius 590 feet at
60 mph? Round your answer to the nearest pound of force.
(Multiple Choice)
4.8/5  (43)
(43)
Graph the polynomial function. Factor first if the expression is not in factored form.
-
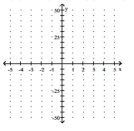
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem
-The area of a square is numerically 5 more than the perimeter. Find the length of the side.
(Multiple Choice)
4.9/5  (33)
(33)
Provide an appropriate response.
-For what value of does the quadratic function have exactly one -intercept?
(Multiple Choice)
4.8/5  (39)
(39)
Round to the nearest tenth unless indicated otherwise.
-At a fixed temperature, the resistance R of a wire varies directly as the length l and inversely as the square of its diameter d. If the resistance is 0.48 ohm when the diameter is 1 mm and the length is
240 cm, what is the resistance when the diameter is 3 mm and the length is 430 cm?
(Multiple Choice)
4.9/5  (39)
(39)
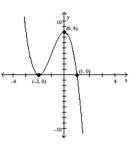
Find a polynomial function f(x) of least possible degree having the graph shown.
-
(Multiple Choice)
4.8/5  (38)
(38)
Find all complex zeros of the polynomial function. Give exact values. List multiple zeros as necessary.
-
(Multiple Choice)
4.9/5  (29)
(29)
Find the equation of the axis of symmetry of the parabola.
-
(Multiple Choice)
4.7/5  (38)
(38)
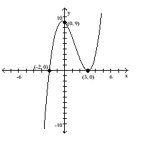
Find a polynomial function f(x) of least possible degree having the graph shown.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find all complex zeros of the polynomial function. Give exact values. List multiple zeros as necessary.
-
(Multiple Choice)
4.8/5  (33)
(33)
Translate the given formula to an English phrase using the word "varies".
-If s varies directly as t2, and s = 567 when t = 9, find s when t is 4.
(Multiple Choice)
4.8/5  (36)
(36)
Provide an appropriate response.
-A quadratic equation f(x) = 0 has a solution x = 3. Its graph has vertex (-1, -16). What is the other solution of the equation?
(Multiple Choice)
4.7/5  (34)
(34)
Find the equation of the axis of symmetry of the parabola.
-
(Multiple Choice)
4.9/5  (39)
(39)
Translate the given formula to an English phrase using the word "varies".
- varies directly as the square of and when . Find when is 9 .
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem
-A can has a surface area of 926 square inches. Its height is inches. What is the radius of the circular top? Round to the nearest hundredth.
(Multiple Choice)
4.7/5  (37)
(37)
Use synthetic division to divide f(x) by x - k for the given value of k. Then express f(x) in the form f(x) = (x - k)q(x) + r for
the given value of k.
-
(Multiple Choice)
4.8/5  (30)
(30)
Showing 361 - 380 of 508
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)