Exam 12: Counting and Probability

Solve the problem. -How many different license plates can be made using 3 letters followed by 4 digits selected from the digits 0 through 9, if digits may be repeated but letters may not be repeated?

Choose the one alternative that best completes the statement or answers the question. -In a survey about the number of siblings of college students, the following probability table was constructed: Number of Siblings Probability 0 0.23 1 0.34 2 0.17 3 0.12 4 or more 0.14 What is the probability that a student has 1, 2, or 3 siblings?

Choose the one alternative that best completes the statement or answers the question. -A bag contains 13 balls numbered 1 through 13. What is the probability of selecting a ball that has an even number when one ball is drawn from the bag?

Write down all the subsets of the given set. - $\{ p , q , r \}$

Solve the problem. -A restaurant offers a choice of 5 salads, 7 main courses, and 3 desserts. How many possible 3-course meals are there?

Solve the problem. -If $n ( A ) = 25 , n ( A \cup B ) = 73$ , and $n ( A \cap B ) = 21$ , find $n ( B )$ .

Write down all the subsets of the given set. - $\{ 1,2,9,11 \}$

Choose the one alternative that best completes the statement or answers the question. -Suppose that the sample space is $S = \{ 1,2,3,4,5,6,7,8,9,10 \rangle$ and that outcomes are equally likely. Compute the probability of the event $E = \{ 2,10 \}$ .

Use the information given in the figure. -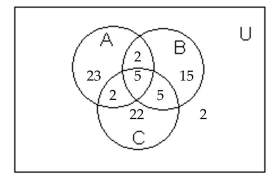 How many are in B but not in A?

Determine whether the following is a probability model. - Outcome Probability Jim 0 Tom 0 Bill 1 Carl 0

Solve the problem. -How many ways are there to choose a soccer team consisting of 3 forwards, 4 midfield players, and 3 defensive players, if the players are chosen from 6 forwards, 7 midfield players, and 5 defensive players?

Choose the one alternative that best completes the statement or answers the question. -Find the probability of getting 2 tails when 3 fair coins are tossed.

Solve the problem. -How many different 8-letter codes are there if only the letters A, B, C, D, E, F, G, H, and I can be used and no letter can be used more than once?

Write the word or phrase that best completes each statement or answers the question. Construct a probability model for the experiment. -Spinner I has 3 sections of equal area, numbered 1, 2, and 3. Spinner II has 3 sections of equal area, labeled Red, Yellow, and Green. Spin Spinner I twice, then Spinner II. What is the probability of getting a 2, followed by a 1, followed by Yellow or Red?

Determine whether the following is a probability model. - Outcome Probability Red 0.16 Blue 0.17 Green 0.25 White 0.27

Choose the one alternative that best completes the statement or answers the question. -Suppose that the sample space is $\mathrm { S } = \{ 1,2,3,4,5,6,7,8,9,10 \}$ and that outcomes are equally likely. Compute the probability of the event $E = \{ 1,2,4,5,7,9,10 \}$ .

Write the word or phrase that best completes each statement or answers the question. Construct a probability model for the experiment. -Rolling a 6-sided fair die twice

Solve the problem. -A committee is to be formed consisting of 2 men and 3 women. If the committee members are to be chosen from 13 men and 9 women, how many different committees are possible?

Find the value of the combination. -C(5, 1)

Solve the problem. -How many different 11-letter words (real or imaginary) can be formed from the letters in the word ENGINEERING?