Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs297 Questions
Exam 2: Linear and Quadratic Functions302 Questions
Exam 3: Polynomial and Rational Functions354 Questions
Exam 4: Exponential and Logarithmic Functions517 Questions
Exam 5: Trigonometric Functions354 Questions
Exam 6: Analytic Trigonometry342 Questions
Exam 7: Applications of Trigonometric Functions105 Questions
Exam 8: Polar Coordinates; Vectors253 Questions
Exam 9: Analytic Geometry200 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability115 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Foundations: a Prelude to Functions234 Questions
Exam 15: Graphing Utilities29 Questions
Select questions type
Choose the one alternative that best completes the statement or answers the question.
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
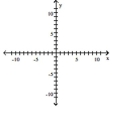
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
D
The graph of a function f is given. Use the graph to answer the question.
-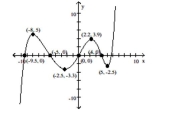 Find the numbers, if any, at which f has a local minimum. What are the local maxima?
Find the numbers, if any, at which f has a local minimum. What are the local maxima?
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
A
Find the average rate of change for the function between the given values.
- ; from 1 to 3
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
D
Solve the problem.
-While traveling at a constant speed in a car, the centrifugal acceleration passengers feel while the car is turning is inversely proportional to the radius of the turn. If the passengers feel an acceleration of 6 feet per second per
Second when the radius of the turn is 50 feet, find the acceleration the passengers feel when the radius of the
Turn is 100 feet.
(Multiple Choice)
4.9/5  (36)
(36)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.9/5  (33)
(33)
Determine whether the equation defines y as a function of x.
-
(Multiple Choice)
4.9/5  (36)
(36)
Choose the one alternative that best completes the statement or answers the question.
-A steel can in the shape of a right circular cylinder must be designed to hold 550 cubic centimeters of juice (see figure). It can be shown that the total surface area of the can (including the ends) is given by ,
where is the radius of the can in centimeters. Using the TABLE feature of a graphing utility, find the radius that minimizes the surface area (and thus the cost) of the can. Round to the nearest tenth of a centimeter.
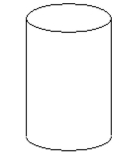
(Multiple Choice)
4.9/5  (30)
(30)
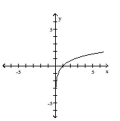
Determine whether the graph is that of a function. If it is, use the graph to find its domain and range, the intercepts, if
any, and any symmetry with respect to the x-axis, the y-axis, or the origin.
-
(Multiple Choice)
4.8/5  (35)
(35)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.9/5  (31)
(31)
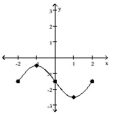
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-
(Multiple Choice)
4.9/5  (54)
(54)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.9/5  (32)
(32)
For the given functions f and g, find the requested function and state its domain.
-
Find .
(Multiple Choice)
4.8/5  (34)
(34)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.8/5  (32)
(32)
Match the graph to the function listed whose graph most resembles the one given.
-
(Multiple Choice)
4.9/5  (29)
(29)
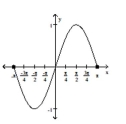
Determine whether the graph is that of a function. If it is, use the graph to find its domain and range, the intercepts, if
any, and any symmetry with respect to the x-axis, the y-axis, or the origin.
-
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-Bob wants to fence in a rectangular garden in his yard. He has 64 feet of fencing to work with and wants to use it all. If the garden is to be feet wide, express the area of the garden as a function of .
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-If , and is undefined, what are the values of and ?
(Multiple Choice)
4.8/5  (31)
(31)
Showing 1 - 20 of 297
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)