Exam 4: Polynomials and Rational Functions
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
A ball is tossed upward. Its height after t seconds is given in the table. Time (seconds) 0.5 1 1.5 2 2.5 Height (feet) 26.5 39.5 44.5 41.5 30.5 Find a quadratic function to model the data. Use the model to determine when the ball reaches its maximum height, as well as the value of the maximum height.
(Multiple Choice)
4.9/5  (42)
(42)
Bob owns a watch repair shop. He has found that the cost of operating his shop is given by , where c is cost and x is the number of watches repaired. How many watches must he repair to have the lowest cost?
(Multiple Choice)
4.8/5  (35)
(35)
Graph the polynomial function. Factor first if the expression is not in factored form.
-
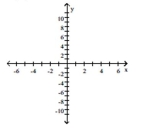
(Multiple Choice)
5.0/5  (27)
(27)
Find all complex zeros of the polynomial function. Give exact values. List multiple zeros as necessary.
-
(Multiple Choice)
4.9/5  (32)
(32)
Use the intermediate value theorem for polynomials to show that the polynomial function has a real zero between the numbers given.
- and
(Multiple Choice)
4.9/5  (38)
(38)
If the average cost per unit C(x) to produce x units of plywood is given by C(x) , what is the unit cost for 20 units?
(Multiple Choice)
4.8/5  (32)
(32)
Use synthetic division to decide whether the given number k is a zero of the given polynomial function.
-k = -1; f(x) = -x4 - 6x2 - x + 4
(True/False)
4.9/5  (31)
(31)
Use the graph to answer the question.
-Find the horizontal and vertical asymptotes of the rational function graphed below.
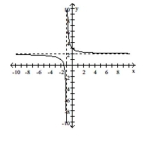
(Multiple Choice)
4.9/5  (39)
(39)
Provide an appropriate response.
-For what values of a does the quadratic function have two -intercepts?
(Multiple Choice)
4.7/5  (28)
(28)
Find an equation for a rational function with the following asymptotes: vertical asymptotes and ,
horizontal asymptote
(Essay)
4.8/5  (32)
(32)
Use the remainder theorem and synthetic division to find f(k).
-
(Multiple Choice)
4.9/5  (33)
(33)
John owns a hot dog stand. He has found that his profit is represented by the equation with P being profits and x the number of hot dogs sold. How many hot dogs must he sell to earn the most profit?
(Multiple Choice)
4.8/5  (31)
(31)
Find a polynomial of least degree with only real coefficients and having the given zeros.
- , and 3
(Multiple Choice)
4.8/5  (35)
(35)
Showing 81 - 100 of 517
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)