Exam 4: Polynomials and Rational Functions
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Use the factor theorem to decide whether or not the second polynomial is a factor of the first.
-
(True/False)
4.7/5  (42)
(42)
Factor f(x) into linear factors given that k is a zero of f(x).
-
(Multiple Choice)
4.9/5  (29)
(29)
Use the boundedness theorem to determine whether the polynomial function satisfies the given condition.
-The polynomial f(x) has no real zero greater than 3.
(Multiple Choice)
4.8/5  (32)
(32)
Use the remainder theorem and synthetic division to find f(k).
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem. Round your answer to two decimal places.
-The weight of a liquid varies directly as its volume V. If the weight of the liquid in a cubical container 5 cm on a side is 375 g, find the weight of the liquid in a cubical container 3 cm on a side.
(Multiple Choice)
4.9/5  (38)
(38)
Find a polynomial of least degree with only real coefficients and having the given zeros.
- , and
(Multiple Choice)
4.8/5  (38)
(38)
Use the equation and the corresponding graph for the quadratic function to find what is requested.
-
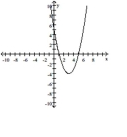 Find the -intercepts.
Find the -intercepts.
(Multiple Choice)
4.9/5  (38)
(38)
Use Descartes' Rule of Signs to determine the possible number of positive real zeros and the possible number of negative real zeros for the function.
-
(Multiple Choice)
4.8/5  (29)
(29)
x and y are two positive numbers and y is three greater than x. The product of the numbers is 130. Find the smaller number, x.
(Multiple Choice)
4.9/5  (35)
(35)
Use Descartes' Rule of Signs to determine the possible number of positive real zeros and the possible number of negative real zeros for the function.
-
(Multiple Choice)
4.9/5  (39)
(39)
Use the boundedness theorem to determine whether the polynomial function satisfies the given condition.
-The polynomial f(x) has no real zero less than -8.
(Multiple Choice)
4.9/5  (38)
(38)
Why does a function defined by a polynomial of degree five with real coefficients have either 1, 3, or 5 real zeros
counting multiplicities?
(Essay)
4.9/5  (31)
(31)
Showing 121 - 140 of 517
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)