Exam 10: Analytic Geometry
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Identify the type of conic section.
-Identify the type of conic section consisting of the set of all points in the plane for which the sum of the distances from the points and is 21 .
(Multiple Choice)
4.8/5  (31)
(31)
Write an equation for the parabola with vertex at the origin.
-Focus
(Multiple Choice)
4.8/5  (33)
(33)
Write an equation for the ellipse.
-eccentricity ; vertices at
(Multiple Choice)
4.7/5  (29)
(29)
Solve the problem.
-The roof of a building is in the shape of the hyperbola , where and are in meters. Refer to the figure and determine the height, , of the outside walls.
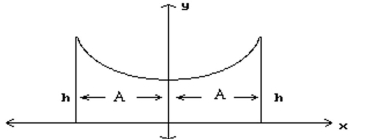
(Multiple Choice)
4.9/5  (37)
(37)
Write an equation for the parabola with vertex at the origin.
-Through , symmetric with respect to the -axis
(Multiple Choice)
4.7/5  (43)
(43)
Identify the equation as a parabola, circle, ellipse, or hyperbola.
-
(Multiple Choice)
4.8/5  (37)
(37)
Write an equation for the hyperbola.
-foci at ; eccentricity
(Multiple Choice)
4.8/5  (31)
(31)
Write the word or phrase that best completes each statement or answers the question.
-Explain the differences between an ellipse and a hyperbola. Both definitions emphasize
distance, but how is distance used differently in these two definitions?
(Essay)
4.9/5  (30)
(30)
Write the word or phrase that best completes each statement or answers the question.
-
(Multiple Choice)
4.9/5  (36)
(36)
Determine the two equations necessary to graph the horizontal parabola using a graphing calculator.
-
(Multiple Choice)
4.8/5  (38)
(38)
Write an equation for the parabola with vertex at the origin.
-Through , opening to the left
(Multiple Choice)
4.9/5  (50)
(50)
Write an equation for the hyperbola.
-center at focus at eccentricity
(Multiple Choice)
4.7/5  (47)
(47)
Solve the problem.
-A domed ceiling is a parabolic surface. For the best lighting on the floor, a light source is to be placed at the focus of the surface. If 9 m down from the top of the dome the ceiling is 8 m wide,
Find the best location for the light source.
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-A projectile is thrown upward so that its distance above the ground after seconds is . After how many seconds does it reach its maximum height?
(Multiple Choice)
4.9/5  (41)
(41)
Showing 41 - 60 of 206
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)