Exam 13: Conic Sections
Exam 1: Review of Real Numbers490 Questions
Exam 2: Equations, Inequalities, and Problem Solving332 Questions
Exam 3: Graphing313 Questions
Exam 4: Solving Systems of Linear Equations146 Questions
Exam 5: Exponents and Polynomials304 Questions
Exam 6: Factoring Polynomials261 Questions
Exam 7: Rational Expressions327 Questions
Exam 8: More on Functions and Graphs192 Questions
Exam 9: Inequalities and Absolute Value148 Questions
Exam 10: Rational Exponents, Radicals, and Complex Numbers379 Questions
Exam 11: Quadratic Equations and Functions242 Questions
Exam 12: Exponential and Logarithmic Functions302 Questions
Exam 13: Conic Sections153 Questions
Exam 14: Sequences, Series, and the Binomial Theorem201 Questions
Select questions type
Sketch the graph of the equation. If the graph is a parabola, find its vertex. If the graph is a circle, find its center and
radius.
-
(Multiple Choice)
4.8/5  (32)
(32)
Solve.
-A bridge constructed over a river has a supporting arch in the shape of a parabola. The length of the road over the parabolic arch is 248 feet and the maximum height of the arch is 112 feet. Write the equation of the arch.
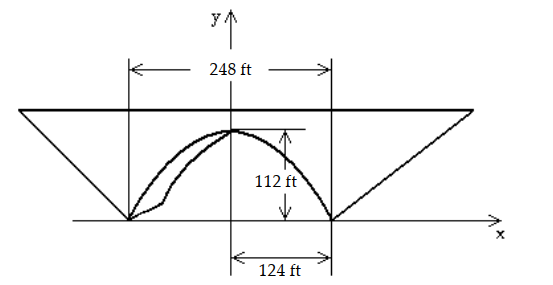
(Multiple Choice)
4.8/5  (40)
(40)
Sketch the graph of the equation. If the graph is a parabola, find its vertex. If the graph is a circle, find its center and
radius.
-

(Multiple Choice)
4.7/5  (32)
(32)
Sketch the graph of the equation. If the graph is a parabola, find its vertex. If the graph is a circle, find its center and
radius.
-
(Multiple Choice)
4.7/5  (38)
(38)
The graph of the equation is a parabola. Determine whether the parabola opens upward, downward, to the left, or to the
right. Do not graph.
-
(Multiple Choice)
4.9/5  (33)
(33)
Fill in the blank with one of the words or phrases listed below. circle ellipse hyperbola conic sections vertex diameter center radius nonlinear system of equations
-Twice a circle's radius is its -----------
(Multiple Choice)
4.8/5  (42)
(42)
Solve the nonlinear system of equations for real solutions.
-
(Multiple Choice)
4.9/5  (35)
(35)
Sketch the graph of the equation. If the graph is a parabola, find its vertex. If the graph is a circle, find its center and
radius.
-
(Multiple Choice)
4.7/5  (37)
(37)
Fill in the blank with one of the words or phrases listed below. circle ellipse hyperbola conic sections vertex diameter center radius nonlinear system of equations
-The circle, parabola, ellipse, and hyperbola are called the --------
(Multiple Choice)
4.8/5  (41)
(41)
The graph of the equation is a parabola. Determine whether the parabola opens upward, downward, to the left, or to the
right. Do not graph.
-
(Multiple Choice)
4.7/5  (33)
(33)
Identify whether the equation, when graphed, will be a parabola, circle, ellipse, or hyperbola.
-
(Multiple Choice)
4.8/5  (37)
(37)
The graph of the equation is a parabola. Determine whether the parabola opens upward, downward, to the left, or to the
right. Do not graph.
-
(Multiple Choice)
5.0/5  (37)
(37)
Solve.
-A planet's orbit about the Sun can be described as an ellipse. Consider the Sun as the origin of a rectangular coordinate system. Suppose that the x-intercepts of the elliptical path of the planet are and that the -intercepts are . Write the equation of the elliptical path of the planet.
(Multiple Choice)
4.8/5  (33)
(33)
Sketch the graph of the equation. If the graph is a parabola, find its vertex. If the graph is a circle, find its center and
radius.
-
(Multiple Choice)
4.8/5  (31)
(31)
Showing 41 - 60 of 153
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)