Exam 12: Exponential Functions and Logarithmic Functions
Exam 1: Introduction to Real Numbers and Algebraic Expressions374 Questions
Exam 2: Solving Equations and Inequalities280 Questions
Exam 3: Graphs of Linear Equations126 Questions
Exam 4: Polynomials: Operations167 Questions
Exam 5: Polynomials: Factoring154 Questions
Exam 6: Rational Expressions and Equations226 Questions
Exam 7: Graphs, Functions, and Applications178 Questions
Exam 8: Systems of Equations118 Questions
Exam 9: More on Inequalities105 Questions
Exam 10: Radical Expressions, Equations, and Functions124 Questions
Exam 11: Quadratic Equations and Functions91 Questions
Exam 12: Exponential Functions and Logarithmic Functions82 Questions
Select questions type
Determine whether the given function is one-to-one. If so, find a formula for the inverse.
-
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
A
Solve the problem.
-An accountant tabulated a firm's profits for four recent years in the following table:
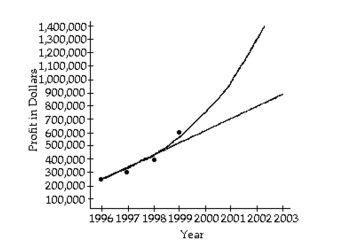
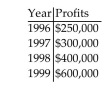 The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the exponential graph to estimate the profits in the year
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the exponential graph to estimate the profits in the year
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
D
Use composition to verify whether or not the inverse is correct.
-
Free
(True/False)
4.8/5  (34)
(34)
Correct Answer:
True
Find the requested composition of functions.
-Given and , find
(Multiple Choice)
4.9/5  (32)
(32)
Find the requested composition of functions.
-Given and , find
(Multiple Choice)
4.8/5  (28)
(28)
Graph the function as a solid curve and its inverse as a dashed curve.
-f(x)= 5x 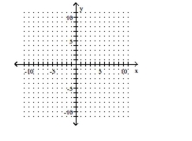
(Multiple Choice)
4.9/5  (32)
(32)
Use composition to verify whether or not the inverse is correct.
-
(True/False)
4.8/5  (31)
(31)
Solve the problem.
-A size dress in Country is size in Country D. A function that converts dress sizes in Country C to those in Country is . Find a formula for the inverse of the function described.
(Multiple Choice)
4.8/5  (37)
(37)
Determine whether the given function is one-to-one. If so, find a formula for the inverse.
-
(Multiple Choice)
4.8/5  (30)
(30)
Determine whether the given function is one-to-one. If so, find a formula for the inverse.
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the requested composition of functions.
-Given and , find
(Multiple Choice)
4.8/5  (38)
(38)
Find an equation of the inverse of the relation.
-y = 2 + 6x
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-An accountant tabulated a firm's profits for four recent years in the following table:
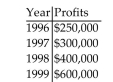 The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year
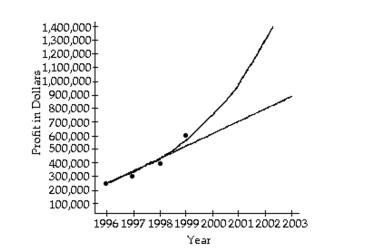
(Multiple Choice)
4.8/5  (29)
(29)
Use composition to verify whether or not the inverse is correct.
-
(True/False)
4.8/5  (39)
(39)
Solve the problem.
-A size 38 dress in Country C is size 11 in Country D. A function that converts dress sizes in Country C to those in Country is . Find a formula for the inverse of the function described.
(Multiple Choice)
4.9/5  (40)
(40)
Showing 1 - 20 of 82
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)