Exam 12: Exponential Functions and Logarithmic Functions
Exam 1: Introduction to Real Numbers and Algebraic Expressions374 Questions
Exam 2: Solving Equations and Inequalities280 Questions
Exam 3: Graphs of Linear Equations126 Questions
Exam 4: Polynomials: Operations167 Questions
Exam 5: Polynomials: Factoring154 Questions
Exam 6: Rational Expressions and Equations226 Questions
Exam 7: Graphs, Functions, and Applications178 Questions
Exam 8: Systems of Equations118 Questions
Exam 9: More on Inequalities105 Questions
Exam 10: Radical Expressions, Equations, and Functions124 Questions
Exam 11: Quadratic Equations and Functions91 Questions
Exam 12: Exponential Functions and Logarithmic Functions82 Questions
Select questions type
Graph the relation using solid circles and the inverse using open circles.
-{(-8, -5), (5, 8), (9, 9), (-9, -9)}
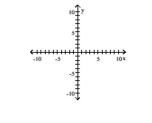
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-A computer is purchased for . Its value each year is about of the value the preceding year. Its value, in dollars, after years is given by the exponential function . Find the value of the computer after 7 years.
(Multiple Choice)
4.7/5  (41)
(41)
Find the requested composition of functions.
-Given and , find .
(Multiple Choice)
4.9/5  (44)
(44)
Determine whether the given function is one-to-one. If so, find a formula for the inverse.
-
(Multiple Choice)
5.0/5  (37)
(37)
Use composition to verify whether or not the inverse is correct.
-
(True/False)
4.8/5  (34)
(34)
Determine whether the given function is one-to-one. If so, find a formula for the inverse.
-
(Multiple Choice)
4.9/5  (33)
(33)
Graph the relation using solid circles and the inverse using open circles.
-{(-10, 14), (-17, -13), (18, 3)}
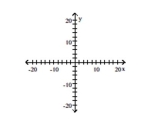
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-The amount of particulate matter left in solution during a filtering process decreases by the equation , where is the number of filtering steps. Find the amounts left for and . (Round to the nearest whole number.)
(Multiple Choice)
4.9/5  (36)
(36)
Graph the function as a solid curve and its inverse as a dashed curve.
-
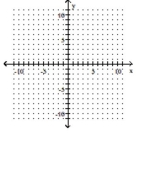
(Multiple Choice)
4.8/5  (30)
(30)
Find the requested composition of functions.
-Given and , find
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-The number of bacteria growing in an incubation culture increases with time according to , where is time in days. Find the number of bacteria when and .
(Multiple Choice)
4.9/5  (35)
(35)
Showing 61 - 80 of 82
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)