Exam 12: Exponential Functions and Logarithmic Functions
Exam 1: Introduction to Real Numbers and Algebraic Expressions374 Questions
Exam 2: Solving Equations and Inequalities280 Questions
Exam 3: Graphs of Linear Equations126 Questions
Exam 4: Polynomials: Operations167 Questions
Exam 5: Polynomials: Factoring154 Questions
Exam 6: Rational Expressions and Equations226 Questions
Exam 7: Graphs, Functions, and Applications178 Questions
Exam 8: Systems of Equations118 Questions
Exam 9: More on Inequalities105 Questions
Exam 10: Radical Expressions, Equations, and Functions124 Questions
Exam 11: Quadratic Equations and Functions91 Questions
Exam 12: Exponential Functions and Logarithmic Functions82 Questions
Select questions type
Solve the problem.
-The half-life of Antimony 111 is hours. If the formula gives the percent (as a decimal) remaining after time (in hours), sketch P versus .
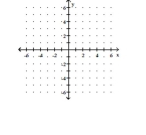
(Multiple Choice)
4.9/5  (26)
(26)
Find the inverse of the relation.
-{(6, -6), (6, -5), (4, -4), (2, -3)}
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-An accountant tabulated a firm's profits for four recent years in the following table: 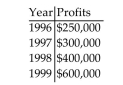 The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year
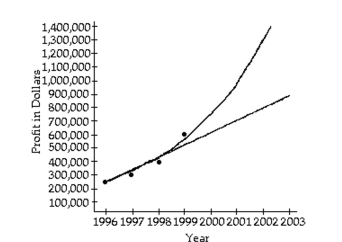
(Multiple Choice)
4.9/5  (29)
(29)
Graph the equation of the relation using a solid line, and then graph the inverse of the relation using a dashed line.
-
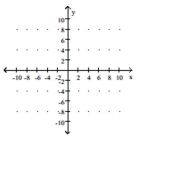
(Multiple Choice)
4.9/5  (33)
(33)
Graph the equation of the relation using a solid line, and then graph the inverse of the relation using a dashed line.
-
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-The half-life of a certain radioactive substance is 22 years. Suppose that at time , there are of the substance. Then after t years, the number of grams of the substance remaining will be:
How many grams of the substance will remain after 242 years? Round to the nearest hundredth when necessary.
(Multiple Choice)
4.7/5  (37)
(37)
Solve the problem.
-Suppose that $90,000 is invested at 4% interest, compounded annually. Find a function A for the amount in the account after t years.
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-A size 10 dress in Country C is size 44 in Country D. A function that converts dress sizes in Country C to those in Country is . Find a formula for the inverse of the function described.
(Multiple Choice)
4.9/5  (34)
(34)
Find the inverse of the relation.
-{(-6, 2), (-2, 6), (9, -2), (-9, 2)}
(Multiple Choice)
4.9/5  (33)
(33)
Use composition to verify whether or not the inverse is correct.
-
(True/False)
4.9/5  (29)
(29)
Find an equation of the inverse of the relation.
-y = 6x + 5
(Multiple Choice)
4.8/5  (43)
(43)
Showing 21 - 40 of 82
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)