Exam 8: Exponential and Logarithmic Functions and Applications
Exam 1: Linear Equations and Inequalities in One Variable151 Questions
Exam 2: Linear Equations in Two Variables and Functions140 Questions
Exam 3: Systems of Linear Equations and Inequalities118 Questions
Exam 4: Polynomials175 Questions
Exam 5: Rational Expressions and Rational Equations121 Questions
Exam 6: Radicals and Complex Numbers168 Questions
Exam 7: Quadratic Equations, Functions and Inequalities121 Questions
Exam 8: Exponential and Logarithmic Functions and Applications144 Questions
Exam 9: Conic Sections80 Questions
Exam 10: Binomial Expansions, Sequences, and Series60 Questions
Exam 11: Online: Transformations, Piecewise-Defined Functions, and Probability83 Questions
Select questions type
If both and are one-to-one functions, and , then which of the following is/are true?
(Multiple Choice)
4.9/5  (42)
(42)
Write the expression as a single logarithm. Assume all variables represent positive real numbers.
(Multiple Choice)
4.8/5  (39)
(39)
Use a calculator to approximate the logarithm. Round to 3 decimal places.
(Multiple Choice)
4.9/5  (37)
(37)
Use the change-of-base formula to approximate the logarithm to four decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
A professor discovers that the GPA of a student at her university can be estimated reasonably well using the formula where h is the total number of hours spent studying outside of class in a semester, d is the number of classes missed during the semester, and G is the student's GPA for the semester. Expand this formula using properties of logs, and use your answer to find the expected semester GPA of a student that studies for 300 hours and misses 2 classes.
(Short Answer)
4.8/5  (33)
(33)
Solve the exponential equation by taking a logarithm of both sides.
(Multiple Choice)
4.8/5  (41)
(41)
Graph the equation by completing the table and plotting points. Round to two decimal places when necessary.
x y 3.5 4 6 8
(Short Answer)
4.9/5  (29)
(29)
In many cases, the population of a town can be predicted using the same formula that is used to compute the balance of an account with interest compounded continuously. If a town has 14,850 citizens now, and grows at 4.5% per year, predict the population in 10 years to the nearest whole number. [Hint: in the formula for continuously-compounded interest, substitute the current population for the principal. The result (amount) will correspond to the new population.]
(Short Answer)
4.8/5  (21)
(21)
Graph the equation by completing the table and plotting points. Round to two decimal places when necessary.
x y 0.5 1 4 8
(Short Answer)
4.9/5  (27)
(27)
Determine if the function is one-to-one by using the horizontal line test. 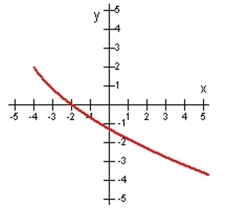
(Multiple Choice)
4.7/5  (22)
(22)
A particular type of radioactive medical waste is shipped to a "cooling-down" facility in sealed plastic barrels where it is housed until the radiation intensity falls below a fixed threshold. Upon arrival, a barrel contains 6 pounds of the radioactive material and must be stored until the radioactive component has decayed to 1 pound or less, after which time the barrel may be shipped out for final disposal. If the amount of radioactive waste in a barrel is given by the formula where t is the number of days after arrival, how long must a barrel be stored before it can be shipped for final disposal? Round to the nearest tenth of a day.
(Short Answer)
4.7/5  (24)
(24)
Showing 101 - 120 of 144
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)