Exam 7: Quadratic Equations, Functions and Inequalities
Exam 1: Linear Equations and Inequalities in One Variable151 Questions
Exam 2: Linear Equations in Two Variables and Functions140 Questions
Exam 3: Systems of Linear Equations and Inequalities118 Questions
Exam 4: Polynomials175 Questions
Exam 5: Rational Expressions and Rational Equations121 Questions
Exam 6: Radicals and Complex Numbers168 Questions
Exam 7: Quadratic Equations, Functions and Inequalities121 Questions
Exam 8: Exponential and Logarithmic Functions and Applications144 Questions
Exam 9: Conic Sections80 Questions
Exam 10: Binomial Expansions, Sequences, and Series60 Questions
Exam 11: Online: Transformations, Piecewise-Defined Functions, and Probability83 Questions
Select questions type
Determine the discriminant. Then use it to determine the number of x-intercepts that the function has.
(Multiple Choice)
4.7/5  (33)
(33)
A model rocket is launched from a raised platform at a speed of 112 feet per second. Its height in feet is given by (t = seconds after launch) What is the maximum height reached by the rocket?
(Multiple Choice)
4.8/5  (36)
(36)
Solve the rational inequality. Write the answer in interval notation.
(Multiple Choice)
4.7/5  (41)
(41)
A cable car carries tourists from street level down into a canyon, as shown in the figure below. The horizontal distance d between the two cable support towers is 450 feet, and the length of the cable between the towers is 3 times the vertical descent h (see figure). Find the vertical descent h into the canyon. Round to the nearest tenth of a foot. 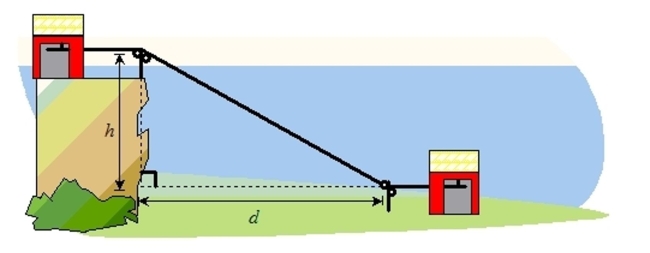
(Short Answer)
4.9/5  (39)
(39)
The daily profit made by an automobile manufacturer is where x is the number of cars produced per shift. How many cars must be produced per shift for the company to make a daily profit of $6000? Round any decimal part up to the next whole car.
(Short Answer)
4.8/5  (35)
(35)
Solve the rational inequality. Write the answer in interval notation.
(Multiple Choice)
4.8/5  (29)
(29)
Use the discriminant to determine the type and number of solutions:
(Multiple Choice)
4.7/5  (32)
(32)
Use the discriminant to determine the type and number of solutions.
(Multiple Choice)
4.7/5  (42)
(42)
Solve the rational inequality. Write the answer in interval notation.
(Multiple Choice)
4.9/5  (37)
(37)
The daily profit in dollars made by an automobile manufacturer is where x is the number of cars produced per shift. How many cars must be produced per shift for the company to maximize its profit?
(Multiple Choice)
4.9/5  (34)
(34)
Showing 21 - 40 of 121
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)