Exam 9: Sequences and Series; Counting and Probability
Exam 1: Equations, Inequalities, and Applications221 Questions
Exam 2: The Rectangular Coordinate System, Lines, and Circles140 Questions
Exam 3: Functions247 Questions
Exam 4: Polynomial and Rational Functions255 Questions
Exam 5: Exponential and Logarithmic Functions and Equations186 Questions
Exam 6: Conic Sections97 Questions
Exam 7: Systems of Equations and Inequalities226 Questions
Exam 8: Matrices83 Questions
Exam 9: Sequences and Series; Counting and Probability255 Questions
Exam 10: Math Exercises: Sets, Intervals, Absolute Value, and Properties298 Questions
Select questions type
Solve the problem.
-How many different 3-letter codes are there if only the letters A, B, C, D, E, F, G, H, and I can be used and no letter can be used more than once?
(Multiple Choice)
4.8/5  (31)
(31)
Use the Venn diagram below to determine the probability. 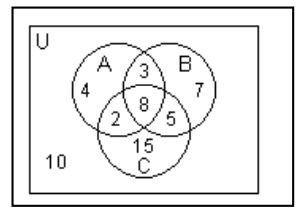 -
-
(Multiple Choice)
5.0/5  (22)
(22)
Find the indicated term of the arithmetic sequence.
-Given an arithmetic sequence with a16 = 19 and a10 = 7, find a4.
(Multiple Choice)
4.9/5  (36)
(36)
Find the probability.
-Two 6-sided dice are rolled. What is the probability the sum of the two numbers on the die will be 6?
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-Seven slips of paper marked with the numbers 1, 2, 3, 4, 5, 6, and 7 are placed in a box and mixed well. Two are drawn. What are the odds that the sum of the numbers on the two selected slips is not 5?
(Multiple Choice)
4.9/5  (39)
(39)
Write the first five terms of the geometric sequence with the given information.
-The first term is -5 and the common ratio is -4.
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-A football player with a field goal kicking percentage of 60% for kicks of 40 yards or less attempts a final-minute field goal of 32 yards. What are the odds of a successful kick?
(Multiple Choice)
4.8/5  (30)
(30)
Determine if the sequence is arithmetic. If the sequence is arithmetic, find the common difference.
-3 , 9 , 27 , 81 , 243, . . .
(Multiple Choice)
4.7/5  (37)
(37)
Find the sum of the geometric series.
-
Express the answer as a fraction.
(Multiple Choice)
4.8/5  (35)
(35)
Find the indicated term or coefficient of the binomial expansion.
-Find the 11th term of the expansion of .
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-A pendulum bob swings through an arc 50 inches long on its first swing. Each swing thereafter, it swings only 70% as far as on the previous swing. How far will it swing altogether before coming to a complete stop?
(Multiple Choice)
4.8/5  (44)
(44)
Find the indicated term or coefficient of the binomial expansion.
-Find the 8 th term of the expansion of .
(Multiple Choice)
4.9/5  (33)
(33)
Write the first four terms of the recursive sequence.
- for
(Multiple Choice)
4.9/5  (34)
(34)
Showing 201 - 220 of 255
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)