Exam 9: Sequences and Series; Counting and Probability
Exam 1: Equations, Inequalities, and Applications221 Questions
Exam 2: The Rectangular Coordinate System, Lines, and Circles140 Questions
Exam 3: Functions247 Questions
Exam 4: Polynomial and Rational Functions255 Questions
Exam 5: Exponential and Logarithmic Functions and Equations186 Questions
Exam 6: Conic Sections97 Questions
Exam 7: Systems of Equations and Inequalities226 Questions
Exam 8: Matrices83 Questions
Exam 9: Sequences and Series; Counting and Probability255 Questions
Exam 10: Math Exercises: Sets, Intervals, Absolute Value, and Properties298 Questions
Select questions type
-An 8-sided die is rolled. The sides contain the numbers 1, 2, 3, 4, 5, 6, 7, 8. State the number of elements in the sample space of rolling one die.
(Multiple Choice)
4.9/5  (32)
(32)
Write the statements S1, S2, and S3 and determine if each statement is true.
-
(Essay)
4.9/5  (35)
(35)
Find the indicated term of the arithmetic sequence.
-7, 2 , -3, -8, . . . ;
(Multiple Choice)
4.7/5  (36)
(36)
Write the first four terms of the recursive sequence.
- for
(Multiple Choice)
4.9/5  (28)
(28)
Solve the problem.
-Lonnie deposits $100 each month into an account paying annual interest of 7% compounded monthly. How much will his account have in it at the end of 10 years? Round to the nearest dollar.
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-A baseball player with a batting average of 0.400 comes to bat. What are the odds of his getting a hit?
(Multiple Choice)
4.9/5  (40)
(40)
Find the indicated term of the arithmetic sequence.
-Given an arithmetic sequence with d = 6 and a5 = 27 , find a20.
(Multiple Choice)
4.9/5  (35)
(35)
Find the probability.
-A bag contains 5 red marbles, 3 blue marbles, and 1 green marble. What is the probability of choosing a marble that is not blue when one marble is drawn from the bag?
(Multiple Choice)
4.8/5  (34)
(34)
Use the principle of mathematical induction to show that the mathematical statement is true for all natural numbers n.
-
(Essay)
4.7/5  (42)
(42)
Solve the problem.
-A card is drawn from a well-shuffled deck of 52 cards. What is the probability of getting a red 6?
(Multiple Choice)
4.8/5  (31)
(31)
Rewrite the series using summation notation. Use 1 as the lower limit of summation.
-
(Multiple Choice)
4.9/5  (41)
(41)
Find the indicated term of the arithmetic sequence.
-Given an arithmetic sequence with a1 = -8 and a8 = 48, find a15.
(Multiple Choice)
4.8/5  (37)
(37)
Rewrite the series using summation notation. Use 1 as the lower limit of summation.
-
(Multiple Choice)
4.7/5  (44)
(44)
Find the indicated sum.
--20 + -30 + -40 + -50 + . . . + a40
(Multiple Choice)
4.7/5  (31)
(31)
Solve the problem.
-As part of her retirement savings plan, Patricia deposited $100 in a bank account during her first year in the workforce. During each subsequent year, she deposited $45 more than the previous year. Find how much she deposited during her twentieth year in the workforce. Find the total amount deposited in the twenty years.
(Multiple Choice)
4.8/5  (39)
(39)
Determine if the sequence is geometric. If the sequence is geometric, find the common ratio.
-3, 12, 48, 192, 768, . . .
(Multiple Choice)
4.9/5  (42)
(42)
Find the probability.
-What is the probability that the arrow will land on an odd number? 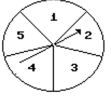
(Multiple Choice)
4.7/5  (37)
(37)
Showing 81 - 100 of 255
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)