Exam 2: Linear and Quadratic Functions
Exam 1: Functions and Their Graphs276 Questions
Exam 2: Linear and Quadratic Functions210 Questions
Exam 3: Polynomial and Rational Functions96 Questions
Exam 5: Conics63 Questions
Exam 6: Systems of Equations and Inequalities134 Questions
Exam 7: Sequences; Induction; the Binomial Theorem104 Questions
Exam 8: Counting and Probability65 Questions
Select questions type
Find the real zeros of the function. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
4.9/5  (36)
(36)
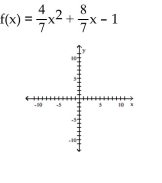
Graph the function f by starting with the graph of y = x2 and using transformations (shifting, compressing, stretching,
and/or reflection).
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-The following data represents the amount of money Tom is saving each month since he graduated from college. month 1 2 3 4 5 6 7 savings \ 52 \ 70 \ 81 \ 91 \ 102 \ 118 \ 132 Find the slope of the line of best fit for the data set and interpret it.
(Essay)
4.9/5  (34)
(34)
Use factoring to find the zeros of the quadratic function. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
4.9/5  (36)
(36)
Determine the quadratic function whose graph is given.
-The quadratic function f(x) = 0.0041x2 - 0.48x + 36.42 models the median, or average, age, y, at which U.S. men were first married x years after 1900. In which year was this average age at a minimum? (Round to the nearest
Year.) What was the average age at first marriage for that year? (Round to the nearest tenth.)
(Multiple Choice)
4.7/5  (33)
(33)
Find the complex zeros of the quadratic function.
Solve the inequality. Express your answer using interval notation. Graph the solution set.
-

(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-Regrind, Inc. regrinds used typewriter platens. The variable cost per platen is $1.50. The total cost to regrind 70 platens is $400. Find the linear cost function to regrind platens. If reground platens sell for $8.40 each, how
Many must be reground and sold to break even?
(Multiple Choice)
4.8/5  (43)
(43)
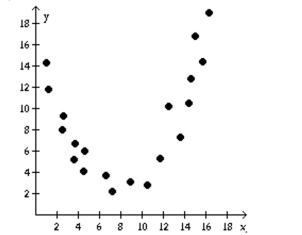
Determine if the type of relation is linear, nonlinear, or none.
-
(Multiple Choice)
4.8/5  (32)
(32)
Determine the quadratic function whose graph is given.
-A projectile is thrown upward so that its distance above the ground after t seconds is h = -10t2 + 320t. After how many seconds does it reach its maximum height?
(Multiple Choice)
4.9/5  (28)
(28)
Determine the quadratic function whose graph is given.
-The number of mosquitoes M(x), in millions, in a certain area depends on the June rainfall x, in inches: M(x) = 12x - x2 . What rainfall produces the maximum number of mosquitoes?
(Multiple Choice)
4.8/5  (37)
(37)
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
- x 3 5 7 15 16 y 8 11 7 14 20
(Multiple Choice)
5.0/5  (31)
(31)
Find the real zeros of the function. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-To convert a temperature from degrees Celsius to degrees Fahrenheit, you multiply the temperature in degrees Celsius by 1.8 and then add 32 to the result. Express F as a linear function of c.
(Multiple Choice)
4.8/5  (33)
(33)
Use a graphing calculator to plot the data and find the quadratic function of best fit.
-An engineer collects data showing the speed s of a given car model and its average miles per gallon M. Use a graphing calculator to plot the scatter diagram. What is the quadratic function of best fit? Speed, s mph, M 20 18 30 20 40 23 50 25 60 28 70 24 80 22
(Multiple Choice)
4.8/5  (28)
(28)
Solve the problem.
-As part of a physics experiment, Ming drops a baseball from the top of a 310-foot building. To the nearest tenth of a second, for how many seconds will the baseball fall? (Hint: Use the formula h = 16t2, which gives the distance h, in feet, that a free-falling object travels in t seconds.)
(Multiple Choice)
4.9/5  (32)
(32)
Determine the slope and y-intercept of the function.
-p(x) = -x + 6
(Multiple Choice)
4.8/5  (38)
(38)
Find the real zeros, if any, of each quadratic function using the quadratic formula. List the x-intercepts, if any, of the
graph of the function.
-
(Multiple Choice)
4.9/5  (31)
(31)
Showing 81 - 100 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)