Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs276 Questions
Exam 2: Linear and Quadratic Functions210 Questions
Exam 3: Polynomial and Rational Functions96 Questions
Exam 5: Conics63 Questions
Exam 6: Systems of Equations and Inequalities134 Questions
Exam 7: Sequences; Induction; the Binomial Theorem104 Questions
Exam 8: Counting and Probability65 Questions
Select questions type
Determine whether the equation defines y as a function of x.
-
(Multiple Choice)
4.7/5  (36)
(36)
Find the value for the function.
-Find -f(x) when f(x) = -2x2 - 5x + 2.
(Multiple Choice)
4.7/5  (27)
(27)
Solve the problem.
-A rectangle that is x feet wide is inscribed in a circle of radius 16 feet. Express the area of the rectangle as a function of x.
(Multiple Choice)
4.9/5  (37)
(37)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.7/5  (39)
(39)
The graph of a function f is given. Use the graph to answer the question.
-How often does the line y = 5 intersect the graph? 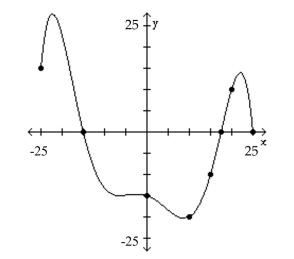
(Multiple Choice)
4.8/5  (36)
(36)
Find the average rate of change for the function between the given values.
-f(x) = 2x - 6; from 1 to 3
(Multiple Choice)
4.7/5  (32)
(32)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-(-2, 0) 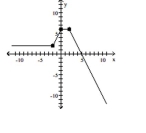
(Multiple Choice)
4.8/5  (44)
(44)
Determine whether the equation defines y as a function of x.
-
(Multiple Choice)
4.9/5  (33)
(33)
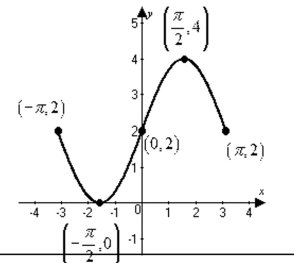
Use the graph to find the intervals on which it is increasing, decreasing, or constant.
-
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-The price and , the quantity of a certain product sold, obey the demand equation
a) Express the revenue R as a function of x.
b) What is the revenue if 450 units are sold?
c) Graph the revenue function using a graphing utility.
d) What quantity x maximizes revenue? What is the maximum revenue?
e) What price should the company charge to maximize revenue?
(Essay)
4.8/5  (43)
(43)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.8/5  (40)
(40)
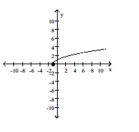
The graph of a function is given. Decide whether it is even, odd, or neither.
-
(Multiple Choice)
4.8/5  (35)
(35)
For the given functions f and g, find the requested function and state its domain.
- f(x)=x+6;g(x)=3 Find f+g
(Multiple Choice)
4.9/5  (30)
(30)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.9/5  (34)
(34)
Match the graph to the function listed whose graph most resembles the one given.
-
(Multiple Choice)
4.8/5  (37)
(37)
Showing 181 - 200 of 276
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)