Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs276 Questions
Exam 2: Linear and Quadratic Functions210 Questions
Exam 3: Polynomial and Rational Functions96 Questions
Exam 5: Conics63 Questions
Exam 6: Systems of Equations and Inequalities134 Questions
Exam 7: Sequences; Induction; the Binomial Theorem104 Questions
Exam 8: Counting and Probability65 Questions
Select questions type
Match the function with the graph that best describes the situation.
-The amount of rainfall as a function of time, if the rain fell more and more softly.
(Multiple Choice)
4.7/5  (34)
(34)
Determine algebraically whether the function is even, odd, or neither.
-f(x) = -2x2 + 9
(Multiple Choice)
4.7/5  (41)
(41)
Solve the problem.
-If the force acting on an object stays the same, then the acceleration of the object is inversely proportional to its mass. If an object with a mass of 18 kilograms accelerates at a rate of 7 meters per second per second by a force,
Find the rate of acceleration of an object with a mass of 9 kilograms that is pulled by the same force.
Meters per second per second
(Multiple Choice)
4.7/5  (29)
(29)
Given the functi is the point (-1, 4) on the graph of f?
- Given the functi , list the x-intercepts, if any, of the graph of f.
(Multiple Choice)
4.8/5  (27)
(27)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.9/5  (38)
(38)
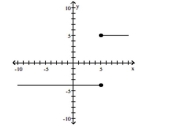
Determine whether the graph is that of a function. If it is, use the graph to find its domain and range, the intercepts, if any, and any symmetry with respect to the x-axis, the y-axis, or the origin.
-
(Multiple Choice)
4.9/5  (33)
(33)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.8/5  (43)
(43)
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local minima. Determine where the function is increasing and where it is decreasing. If necessary, round answers to two
decimal places.
-
(Essay)
4.9/5  (34)
(34)
 For the function, find the average rate of change of f from 1 to x:
-
For the function, find the average rate of change of f from 1 to x:
-
(Multiple Choice)
4.8/5  (38)
(38)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-(1, 5) 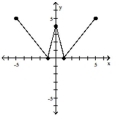
(Multiple Choice)
4.8/5  (47)
(47)
Find the average rate of change for the function between the given values.
-
(Multiple Choice)
4.9/5  (35)
(35)
Determine whether the equation defines y as a function of x.
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the average rate of change for the function between the given values.
-
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-A rectangular box with volume 268 cubic feet is built with a square base and top. The cost is $1.50 per square foot for the top and the bottom and $2.00 per square foot for the sides. Let x represent the length of a side of the
Base. Express the cost the box as a function of x.
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-From a 18-inch by 18-inch piece of metal, squares are cut out of the four corners so that the sides can then be folded up to make a box. Let x represent the length of the sides of the squares, in inches, that are cut out. Express
The volume of the box as a function of x.
(Multiple Choice)
4.9/5  (35)
(35)
The graph of a function f is given. Use the graph to answer the question.
-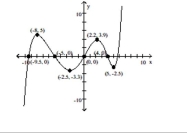 Find the numbers, if any, at which f has a local minimum. What are the local maxima?
Find the numbers, if any, at which f has a local minimum. What are the local maxima?
(Multiple Choice)
4.8/5  (34)
(34)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
(Multiple Choice)
5.0/5  (42)
(42)
Showing 141 - 160 of 276
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)