Exam 9: Differential Equations
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
The population of a certain community is increasing at a rate directly proportional to the population at any time t. In the last 1 yr, the population has doubled. How long will it take for the population to triple? Round the answer to the nearest hundredth, if necessary. __________ yr(s)
Free
(Short Answer)
4.8/5  (39)
(39)
Correct Answer:
1.58
y is a solution of the differential equation.
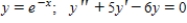
Free
(True/False)
4.9/5  (37)
(37)
Correct Answer:
False
The rate at which a rumor spreads through an Alpine village of 500 residents is jointly proportional to the number of residents who have heard it and the number who have not. Initially, 15 residents heard the rumor, but 4 days later this number increased to 80. Find the number of people who will have heard the rumor after 1 wk. Round the answer to the nearest integer. __________ people
Free
(Short Answer)
4.8/5  (28)
(28)
Correct Answer:
213
Consider the differential equation 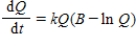 with the side condition
with the side condition 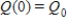 . The solution Q(t) describes restricted growth and has a graph known as the Gompertz curve. Using separation of variables, solve this differential equation.
. The solution Q(t) describes restricted growth and has a graph known as the Gompertz curve. Using separation of variables, solve this differential equation.
(Short Answer)
4.8/5  (34)
(34)
Two chemical solutions, one containing N molecules of chemical A and another containing M molecules of chemical B, are mixed together at time t = 0. The molecules from the two chemicals combine to form another chemical solution containing y (AB) molecules. The rate at which the AB molecules are formed, 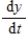 , is called the reaction rate and is jointly proportional to
, is called the reaction rate and is jointly proportional to 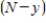 and
and 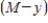 . Thus,
. Thus, 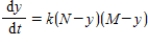 where k is a constant (we assume the temperature of the chemical mixture remains constant during the interaction). Solve this differential equation with the side condition
where k is a constant (we assume the temperature of the chemical mixture remains constant during the interaction). Solve this differential equation with the side condition 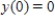 assuming that
assuming that 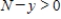 and
and 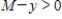
(Short Answer)
4.8/5  (30)
(30)
The personnel manager of Gibraltar Insurance Company estimates that the number of insurance claims an experienced clerk can process in a day is 50. Furthermore, the rate at which a clerk can process insurance claims during the t th wk of training is proportional to the difference between the maximum number possible (50) and the number he or she can process in the t th wk. If the number of claims the average trainee can process after 1 wk on the job is 20/day, determine how many claims the average trainee can process after 7 wk on the job. Round the answer to the nearest integer. __________ claims
(Short Answer)
5.0/5  (37)
(37)
Use Euler's method with given values of n to obtain an approximation of the initial value problem when 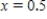 . Round your answers to four decimal places, if necessary.
. Round your answers to four decimal places, if necessary.
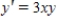 ,
, 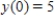
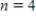 ,
, 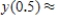 __________
__________
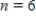 ,
, 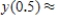 __________
__________
(Short Answer)
4.9/5  (30)
(30)
Find the general solution of the first-order differential equation by separating variables.
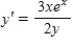
(Short Answer)
4.8/5  (37)
(37)
Find the general solution of the first-order differential equation by separating variables.
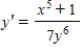
(Short Answer)
4.9/5  (42)
(42)
Use Euler's method with given values of n to obtain an approximation of the initial value problem when 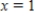 . Round your answers to four decimal places, if necessary.
. Round your answers to four decimal places, if necessary.
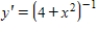 ,
, 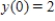
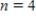 ,
, 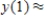 __________
__________
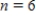 ,
, 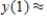 __________
__________
(Short Answer)
4.8/5  (47)
(47)
Suppose a country's population at any time t grows in accordance with the rule 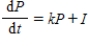 where P denotes the population at any time t, k is a positive constant reflecting the natural growth rate of the population, and I is a constant giving the (constant) rate of immigration into the country. The population of the United States in the year 1980
where P denotes the population at any time t, k is a positive constant reflecting the natural growth rate of the population, and I is a constant giving the (constant) rate of immigration into the country. The population of the United States in the year 1980 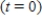 was 224.5 million. Suppose the natural growth rate is 0.8% annually
was 224.5 million. Suppose the natural growth rate is 0.8% annually 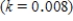 and net immigration is allowed at the rate of 0.5 million people/year
and net immigration is allowed at the rate of 0.5 million people/year 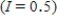 until the end of the century. What will be the U.S. population in 2003? Round the answer to the nearest tenth of a million, if necessary. P=__________ million
until the end of the century. What will be the U.S. population in 2003? Round the answer to the nearest tenth of a million, if necessary. P=__________ million
(Short Answer)
4.9/5  (40)
(40)
Use Euler's method with given values of n to obtain an approximation of the initial value problem when 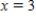 . Round your answers to four decimal places, if necessary.
. Round your answers to four decimal places, if necessary.
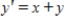 ,
, 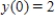
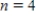 ,
, 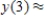 __________
__________
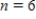 ,
, 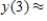 __________
__________
(Short Answer)
4.9/5  (31)
(31)
Find the general solution of the first-order differential equation by separating variables.
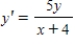
(Short Answer)
4.9/5  (31)
(31)
Use Euler's method with given values of n to obtain an approximation of the initial value problem when 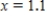 . Round your answers to four decimal places, if necessary.
. Round your answers to four decimal places, if necessary.
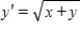 ,
, 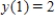
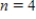 ,
, 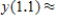 __________
__________
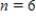 ,
, 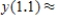 __________
__________
(Short Answer)
4.9/5  (30)
(30)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function 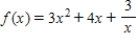 is a solution of the differential equation
is a solution of the differential equation 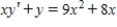
(True/False)
5.0/5  (40)
(40)
Showing 1 - 20 of 57
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)