Exam 11: Taylor Polynomials and Infinite Series
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
Use the Newton method to approximate the indicated zero of the function. Continue with the iteration until two successive approximations differ by less than 0.0001. Round your answer to five decimal places, if necessary.
The zero of 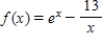 between
between 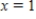 and
and 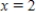 ,
, 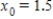 .
.
Free
(Short Answer)
4.9/5  (24)
(24)
Correct Answer:
1.91515
Consider the function 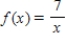 at
at 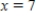 .
Find the Taylor series of the function at the indicated point.
__________
Find its radius of convergence.
__________
Find the interval of convergence.
__________
.
Find the Taylor series of the function at the indicated point.
__________
Find its radius of convergence.
__________
Find the interval of convergence.
__________
Free
(Short Answer)
4.8/5  (30)
(30)
Correct Answer:
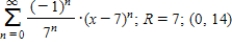
Consider the function 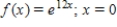 .
Find the Taylor series of the function at the indicated point.
__________
Find its radius of convergence.
__________
Find the interval of convergence.
__________
.
Find the Taylor series of the function at the indicated point.
__________
Find its radius of convergence.
__________
Find the interval of convergence.
__________
Free
(Short Answer)
4.9/5  (36)
(36)
Correct Answer:
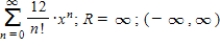
Find P3(x), the third Taylor polynomial of the following function at the indicated point.
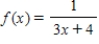 at
at 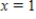
Express any non-integer coefficients as reduced fractions.
Express any non-integer coefficients as reduced fractions.
(Short Answer)
4.8/5  (29)
(29)
Consider the series
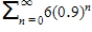 .
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
.
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
(Short Answer)
4.8/5  (26)
(26)
Consider the function 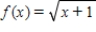 at
at 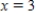 .
Use the second Taylor polynomial to approximate
.
Use the second Taylor polynomial to approximate 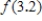 . Round the answer to six decimal places, if necessary.
. Round the answer to six decimal places, if necessary.
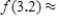 __________
Find a bound for the error in the approximation. Round the answer to five decimal places, if necessary.
__________
__________
Find a bound for the error in the approximation. Round the answer to five decimal places, if necessary.
__________
(Short Answer)
4.8/5  (36)
(36)
Estimate the value of the radical by using three iterations of the Newton-Raphson method with the indicated initial guess for the function. Round your answer to six decimal places, if necessary.
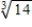 ;
; 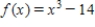 ;
; 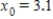
(Short Answer)
4.9/5  (35)
(35)
Estimate the value of the radical by using three iterations of the Newton-Raphson method with the indicated initial guess for the function. Round your answer to six decimal places, if necessary.
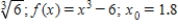
(Short Answer)
4.7/5  (38)
(38)
Consider the series
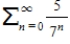 .
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
.
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
(Short Answer)
4.9/5  (36)
(36)
Consider the series 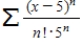 .
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
.
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
(Short Answer)
4.9/5  (39)
(39)
Consider the series
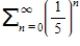 .
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
.
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
(Short Answer)
4.8/5  (39)
(39)
A division manufactures the "Futura" model microwave oven. Given that the daily cost of producing these microwave ovens (in dollars) obeys the rule
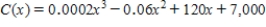
where x stands for the number of units produced, find the level of production that minimizes the daily average cost per unit. Round your answer to the nearest integer.
__________ units per day
where x stands for the number of units produced, find the level of production that minimizes the daily average cost per unit. Round your answer to the nearest integer.
__________ units per day
(Short Answer)
4.8/5  (34)
(34)
Consider the series 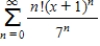 .
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
.
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
(Short Answer)
4.8/5  (34)
(34)
The altitude (in feet) of a rocket t sec into flight is given by
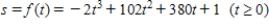
Find the time T when the rocket hits Earth. Round your answer to the nearest second.
Find the time T when the rocket hits Earth. Round your answer to the nearest second.
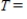 __________ sec
__________ sec
(Short Answer)
4.7/5  (39)
(39)
Consider the series
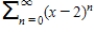 .
Find the values of x for which the series converges.
Find the sum of the series where it is convergent
.
Find the values of x for which the series converges.
Find the sum of the series where it is convergent
(Short Answer)
4.9/5  (35)
(35)
Determine whether the following series is convergent or divergent.
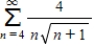
(Short Answer)
4.7/5  (33)
(33)
Showing 1 - 20 of 110
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)