Exam 4: Applications of the Derivative
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 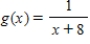 on
on 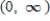
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
D
Find the horizontal and vertical asymptotes of the graph of the function. 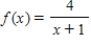
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
D
Find the relative maxima and relative minima, if any, of the function. 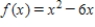
Free
(Multiple Choice)
4.8/5  (43)
(43)
Correct Answer:
C
Find the relative extrema, if any, of the function. Use the second derivative test, if applicable. 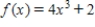
(Multiple Choice)
4.9/5  (43)
(43)
In the diagram, S represents the position of a power relay station located on a straight coast, and E shows the location of a marine biology experimental station on an island. A cable is to be laid connecting the relay station with the experimental station. 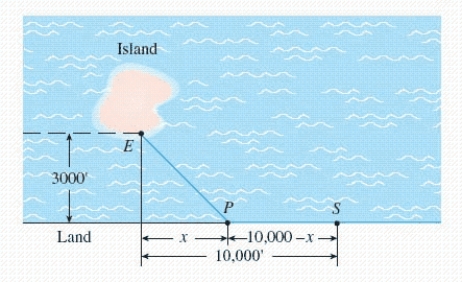
If the cost of running the cable on land is $2.00/running foot and the cost of running the cable under water is $5.20/running foot, locate the point P that will result in a minimum cost (solve for x).
If the cost of running the cable on land is $2.00/running foot and the cost of running the cable under water is $5.20/running foot, locate the point P that will result in a minimum cost (solve for x).
(Multiple Choice)
4.7/5  (33)
(33)
Determine where the function is concave upward and where it is concave downward. 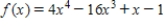
(Multiple Choice)
4.7/5  (32)
(32)
The owner of the Rancho Los Feliz has 3,200 yd of fencing material with which to enclose a rectangular piece of grazing land along the straight portion of a river. If fencing is not required along the river, what are the dimensions of the largest area that he can enclose? What is this area?
(Multiple Choice)
4.7/5  (37)
(37)
By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made. If the cardboard is 8 in. long and 3 in. wide, find the dimensions of the box that will yield the maximum volume.
(Multiple Choice)
4.8/5  (36)
(36)
Select the graph of the function using the curve-sketching guide. 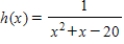
(Multiple Choice)
4.9/5  (37)
(37)
The total annual revenue R of the Miramar Resorts Hotel is related to the amount of money x the hotel spends on advertising its services by the function 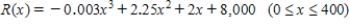 where both R and x are measured in thousands of dollars.
Use this function to:
1) Find the interval where the graph of R is concave upward and the interval where the graph of R is concave downward.
2) Find the inflection point of R.
3) Determine if it would it be more beneficial for the hotel to increase its advertising budget slightly when the budget is $240,000 or when it is $260,000.
where both R and x are measured in thousands of dollars.
Use this function to:
1) Find the interval where the graph of R is concave upward and the interval where the graph of R is concave downward.
2) Find the inflection point of R.
3) Determine if it would it be more beneficial for the hotel to increase its advertising budget slightly when the budget is $240,000 or when it is $260,000.
(Multiple Choice)
4.9/5  (38)
(38)
You are given the graph of some function f defined on the indicated interval. Find the absolute maximum and the absolute minimum of f, if they exist. 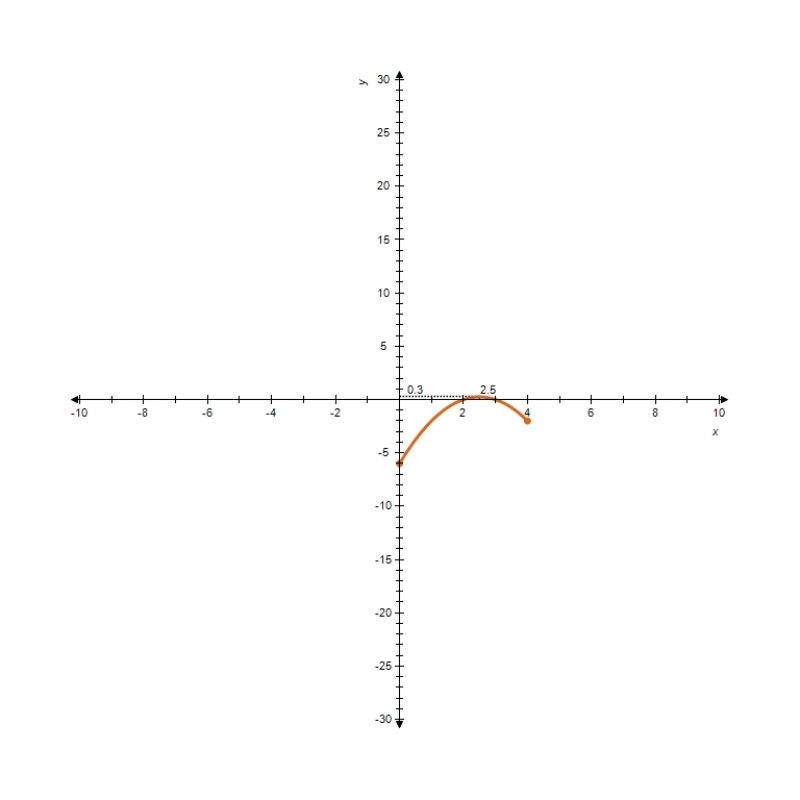
F defined on
F defined on 
(Multiple Choice)
4.9/5  (42)
(42)
Show that the function 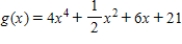 is concave upward wherever it is defined.
is concave upward wherever it is defined.
(Multiple Choice)
4.8/5  (38)
(38)
Find the relative extrema, if any, of the function. Use the second derivative test, if applicable. 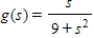
(Multiple Choice)
4.8/5  (48)
(48)
You are given the graph of a function
Determine the intervals where f is concave downward. 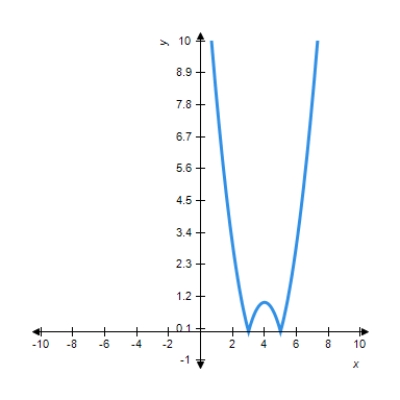
(Multiple Choice)
4.9/5  (34)
(34)
Find the relative extrema, if any, of the function. Use the second derivative test, if applicable. 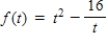
(Multiple Choice)
4.8/5  (36)
(36)
The quantity demanded each month of the Sicard wristwatch is related to the unit price by the equation 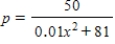
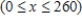 , where
, where 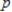 is measured in dollars and
is measured in dollars and  is measured in units of a thousand.
To yield a maximum revenue, how many watches must be sold?
is measured in units of a thousand.
To yield a maximum revenue, how many watches must be sold?
 __________
__________
(Short Answer)
4.9/5  (38)
(38)
A division of Chapman Corporation manufactures a pager. The weekly fixed cost for the division is $20,000, and the variable cost for producing  pagers/week is
pagers/week is 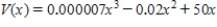 dollars. The company realizes a revenue of
dollars. The company realizes a revenue of 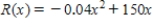
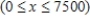 dollars from the sale of
dollars from the sale of  pagers/week.
Find the level of production that will yield a maximum profit for the manufacturer.
pagers/week.
Find the level of production that will yield a maximum profit for the manufacturer.
(Short Answer)
4.8/5  (39)
(39)
Showing 1 - 20 of 152
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)