Exam 18: Advanced Time Series Topics
Exam 1: The Nature of Econometrics and Economic Data28 Questions
Exam 2: The Simple Regression Model30 Questions
Exam 3: Multiple Regression Analysis Estimation28 Questions
Exam 4: Multiple Regression Analysis Inference28 Questions
Exam 5: Multiple Regression Analysis Ols Asymptotics25 Questions
Exam 6: Multiple Regression Analysis Further Issues27 Questions
Exam 7: Multiple Regression Analysis With Qualitative Information28 Questions
Exam 8: Heteroskedasticity27 Questions
Exam 9: More on Specification and Data Issues27 Questions
Exam 10: Basic Regression Analysis With Time Series Data27 Questions
Exam 11: Further Issues in Using Ols With Time Sries Data28 Questions
Exam 12: Serial Correlation and Heteroskedasticity in Time Series Regressions26 Questions
Exam 13: Pooling Cross Sections Across Time Simple Panel Data Methods28 Questions
Exam 14: Advanced Panel Data Methods27 Questions
Exam 15: Instrumental Variables Estimation and Two Strage Least Squares29 Questions
Exam 16: Simultaneous Equations Models25 Questions
Exam 17: Limited Dependent Variable Models and Sample Selection Correctons25 Questions
Exam 18: Advanced Time Series Topics25 Questions
Exam 19: Carrying Out an Empirical Project25 Questions
Select questions type
Which of the following statements is true?
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
C
The Koyck distributed lag model is an example of:
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
C
A spurious regression refers to a situation where:
Free
(Multiple Choice)
4.7/5  (35)
(35)
Correct Answer:
B
The long-run propensity measures the long-run change in the expected value of y given a one-unit, permanent increase in z.
(True/False)
4.8/5  (22)
(22)
If the t statistic for the presence of a unit root in a variable is −7.22 and the 5% critical value is −2.86, there is strong evidence against a unit root in the variable.
(True/False)
4.8/5  (26)
(26)
Vector autoregressive models should be used for forecasting if the series being studied are cointegrated.
(True/False)
4.8/5  (38)
(38)
If two series have means that are not trending, a simple regression involving two independent I(1) series will often result in a significant _____ statistic.
(Multiple Choice)
4.9/5  (33)
(33)
Exponential smoothing is a forecasting method where the weights on the lagged dependent variable decline to zero exponentially.
(True/False)
4.9/5  (36)
(36)
The R2 calculated in a spurious regression is a valid and efficient estimate of the goodness-of-fit of the regression equation.
(True/False)
4.8/5  (42)
(42)
The model: yt =  0 +
0 +  0zt +
0zt + 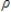 yt - 1 +
yt - 1 +  1zt - 1 +vt, where vt = ut -
1zt - 1 +vt, where vt = ut - 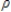 ut - 1 represents a:
ut - 1 represents a:
(Multiple Choice)
4.9/5  (33)
(33)
Let {(yt, zt): t = …, −2,−1, 0, 1, 2, …} be a bivariate time series process. The model: yt =  +
+  0zt +
0zt +  1zt - 1 +
1zt - 1 +  2zt - 2 + ….. + ut, represents a(n):
2zt - 2 + ….. + ut, represents a(n):
(Multiple Choice)
5.0/5  (29)
(29)
In calculation of squared forecast errors, an error of +3 yields a loss three times greater than an error of −1.
(True/False)
4.9/5  (41)
(41)
For 2.5% significance level, the asymptotic critical value for cointegration test with linear time trend is -3.59.
(True/False)
4.8/5  (29)
(29)
In the given AR(1) model, yt =  +
+ 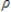 yt - 1 +
yt - 1 +  , t = 1,2…… , the Dickey-Fuller distribution refers to the:
, t = 1,2…… , the Dickey-Fuller distribution refers to the:
(Multiple Choice)
4.7/5  (28)
(28)
A process {yt} is a martingale if _____ is equal to yt for all t ≥ 0.
(Multiple Choice)
4.8/5  (35)
(35)
Which of the following statements correctly identifies the difference between an autoregressive model and a vector autoregressive model?
(Multiple Choice)
4.7/5  (40)
(40)
Which of the following is used to test whether a time series follows a unit root process?
(Multiple Choice)
4.7/5  (44)
(44)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)