Exam 10: Basic Regression Analysis With Time Series Data
Exam 1: The Nature of Econometrics and Economic Data28 Questions
Exam 2: The Simple Regression Model30 Questions
Exam 3: Multiple Regression Analysis Estimation28 Questions
Exam 4: Multiple Regression Analysis Inference28 Questions
Exam 5: Multiple Regression Analysis Ols Asymptotics25 Questions
Exam 6: Multiple Regression Analysis Further Issues27 Questions
Exam 7: Multiple Regression Analysis With Qualitative Information28 Questions
Exam 8: Heteroskedasticity27 Questions
Exam 9: More on Specification and Data Issues27 Questions
Exam 10: Basic Regression Analysis With Time Series Data27 Questions
Exam 11: Further Issues in Using Ols With Time Sries Data28 Questions
Exam 12: Serial Correlation and Heteroskedasticity in Time Series Regressions26 Questions
Exam 13: Pooling Cross Sections Across Time Simple Panel Data Methods28 Questions
Exam 14: Advanced Panel Data Methods27 Questions
Exam 15: Instrumental Variables Estimation and Two Strage Least Squares29 Questions
Exam 16: Simultaneous Equations Models25 Questions
Exam 17: Limited Dependent Variable Models and Sample Selection Correctons25 Questions
Exam 18: Advanced Time Series Topics25 Questions
Exam 19: Carrying Out an Empirical Project25 Questions
Select questions type
The model: Yt = 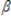 0 +
0 + 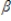 1ct + ut, t = 1,2,……., n is an example of a(n):
1ct + ut, t = 1,2,……., n is an example of a(n):
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
B
Dummy variables can be used to address the problem of seasonality in regression models.
Free
(True/False)
4.9/5  (36)
(36)
Correct Answer:
True
Consider the following equation: Log(yt )= 0.7 + 1.2log(st ) + 0.3log(st-1) + 0.2log(st-2) + 0.1log(st-3)
What is the percentage increase in y given a permanent 1% increase in s?
Free
(Multiple Choice)
4.8/5  (26)
(26)
Correct Answer:
B
Which of the following correctly identifies a difference between cross-sectional data and time series data?
(Multiple Choice)
4.9/5  (35)
(35)
If an explanatory variable is strictly exogenous it implies that:
(Multiple Choice)
4.9/5  (33)
(33)
Which of the following is an assumption on which time series regression is based?
(Multiple Choice)
4.9/5  (34)
(34)
When a series has the same average growth rate from period to period, then it can be approximated by an exponential trend.
(True/False)
4.9/5  (27)
(27)
Adding a time trend can make an explanatory variable more significant if:
(Multiple Choice)
4.9/5  (39)
(39)
Time series regression is based on series which exhibit serial correlation.
(True/False)
4.9/5  (34)
(34)
With base year 1990, the index of industrial production for the year 1999 is 112. What will be the value of the index in 1999, if the base year is changed to 1982 and the index measured 96 in 1982?
(Multiple Choice)
5.0/5  (38)
(38)
Which of the following rules out perfect collinearity among the regressors?
(Multiple Choice)
4.8/5  (31)
(31)
Refer to the following model. yt =  0 +
0 + 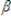 0st +
0st + 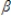 1st-1 +
1st-1 + 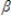 2st-2 +
2st-2 + 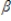 3st-3 + ut
3st-3 + ut 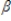 0 +
0 + 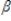 1 +
1 + 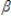 2 +
2 + 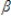 3 represents:
3 represents:
(Multiple Choice)
4.8/5  (33)
(33)
If 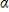 1 > 0, then yt in the linear function of time E(yt) =
1 > 0, then yt in the linear function of time E(yt) = 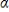 0 +
0 + 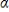 1t displays a(n):
1t displays a(n):
(Multiple Choice)
4.8/5  (29)
(29)
Refer to the following model
yt = 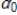 +
+ 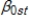 +
+ 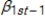 +
+ 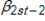 +
+ 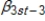 + ut.
Given a permanent increase in s,
+ ut.
Given a permanent increase in s, 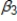 is the long-run propensity.
is the long-run propensity.
(True/False)
4.8/5  (29)
(29)
In a static model, one or more explanatory variables affect the dependent variable with a lag.
(True/False)
4.8/5  (41)
(41)
Supposed that you are interested in estimating country-level maternal mortality rate (mmrt) based just on the gross domestic product per capita (gdppct) and literacy rate (lrt) and you find that countries that have unusually high (for the given levels of gdppc and lr) mmr in one period also have unusually high mmr in the next period. Which of the following assumption for time series analysis does not hold?
(Multiple Choice)
4.9/5  (43)
(43)
Showing 1 - 20 of 27
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)